Question

19．已知函数f（x）=x²-2ax-2alnx（a∈R），则下列说法正确的是①③④．
①当a＜0时，函数y=f（x）有零点；
②若函数y=f（x）有零点，则a＜0；
③存在a＞0，函数y=f（x）有唯一的零点；
④若函数y=f（x）有唯一的零点，则a≤1．

Answer 1

分析 先将函数进行参变量分离，得到2a=$\frac{{x}^{2}}{x+lnx}$，令g（x）=$\frac{{x}^{2}}{x+lnx}$，转化成y=2a与y=g（x）的图象的交点个数，利用导数得到函数的单调性，结合函数的图象可得结论．

解答 解：令f（x）=x²-2ax-2alnx=0，则2a（x+lnx）=x²，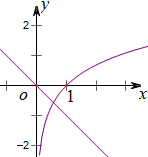
∴2a=$\frac{{x}^{2}}{x+lnx}$，令g（x）=$\frac{{x}^{2}}{x+lnx}$，
则g′（x）=$\frac{2x（x+lnx）-{x}^{2}（1+\frac{1}{x}）}{（x+lnx）^{2}}$=$\frac{x（x-1+2lnx）}{（x+lnx）^{2}}$
令h（x）=x+lnx，通过作出两个函数y=lnx及y=-x的图象（如右图）发现h（x）有唯一零点在（0，1）上，
设这个零点为x₀，当x∈（0，x₀）时，g′（x）＜0，g（x）在（0，x₀）上单调递减，x=x₀是渐近线，
当x∈（x₀，1）时，g′（x）＜0，则g（x）在（x₀，1）上单调递减，
当x∈（1，+∞）时g′（x）＞0，g（x）在（1，+∞）单调递增，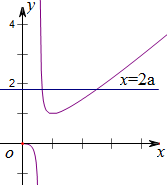
∴g（1）=1，可以作出g（x）=$\frac{{x}^{2}}{x+lnx}$的大致图象，
结合图象可知，当a＜0时，y=2a与y=g（x）的图象只有一个交点，
则函数y=f（x）只有一个零点，故选项A正确；
若函数y=f（x）有零点，则a＜0或a≥$\frac{1}{2}$，故选项B不正确；
存在a=$\frac{1}{2}$＞0，函数y=f（x）有唯一零点，故选项C正确；
若函数y=f（x）有唯一零点，则a＜0，或a=$\frac{1}{2}$，则a≤1，故选项D正确．
故答案为：①③④．

点评 本题考查了函数的零点与方程根的关系．函数的零点等价于对应方程的根，等价于函数的图象与x轴交点的横坐标，解题时要注意根据题意合理的选择转化．常运用数形结合的数学思想方法．属于中档题．