题目内容
函数f(x)＝x3－3a2x＋a(a>0)的极大值为正数，极小值为负数，则a的取值范围为________．
f′(x)＝3x2－3a2(a>0)，
由f′(x)>0，得x>a或x<－a，由f′(x)<0，得－a<x<a.
所以f(x)在(－∞，－a)上递增，(－a，a)上递减，(a，＋∞)上递增．
当x＝－a时，f(x)取得极大值f(－a)＝2a3＋a>0；
当x＝a时，f(x)取得极小值f(a)＝－2a3＋a<0.
又a>0，∴a>
.
由f′(x)>0，得x>a或x<－a，由f′(x)<0，得－a<x<a.
所以f(x)在(－∞，－a)上递增，(－a，a)上递减，(a，＋∞)上递增．
当x＝－a时，f(x)取得极大值f(－a)＝2a3＋a>0；
当x＝a时，f(x)取得极小值f(a)＝－2a3＋a<0.
又a>0，∴a>
.
练习册系列答案
相关题目
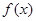为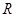
上的可导函数,且
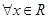,均有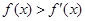
,则以下判断正确的是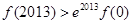
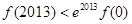
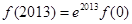
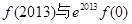大小无法确定
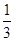x3－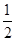
ax2＋(a－1)x＋1在区间(1，4)上是减函数，在区间(6，＋∞)上是增函数，则实数a的取值范围是________．
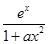，其中a为正实数．
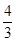时，求f(x)的极值点；②若f(x)为R上的单调函数，求a的取值范围．
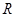上的函数
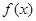，其导函数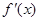
的图像如图所示，则下列叙述正确的是（ ）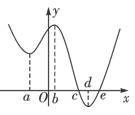
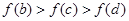
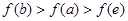
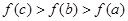
的单调递增区间为( ) 
和
