题目内容
20.已知直线l的参数方程是$\left\{\begin{array}{l}x=\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t+4\sqrt{2}\end{array}$(t是参数),⊙C的极坐标方程为ρ=2$\sqrt{2}cos(θ+\frac{π}{4})$.(Ⅰ)求圆心C的直角坐标;
(Ⅱ)试判断直线l与⊙C的位置关系.
分析 (Ⅰ)化简基本方程为普通方程,然后求解圆心C的直角坐标;
(Ⅱ)求出直线的参数方程,利用圆心到直线的距离,判断直线l与⊙C的位置关系.
解答 (本小题满分10分)
解:(I)由⊙C的极坐标方程为$ρ=2\sqrt{2}cos(θ+\frac{π}{4})$,
展开化为${ρ^2}=2\sqrt{2}ρcos(θ+\frac{π}{4})=2ρ(cosθ-sinθ)$,
即x2+y2=2x-2y,
化为(x-1)2+(y+1)2=2
∴圆心C(1,-1).…(5分)
(II)由直线l的参数方程$\left\{\begin{array}{l}x=\frac{\sqrt{2}}{2}t\\ y=\frac{\sqrt{2}}{2}t+4\sqrt{2}\end{array}\right.$(t是参数),消去参数t可得x-y-4$\sqrt{2}$=0,
∴圆心C到直线的距离$d=\frac{{|{2-4\sqrt{2}}|}}{{\sqrt{2}}}=4-\sqrt{2}>\sqrt{2}$,
因此直线l与圆相离.….(10分)
点评 本题考查参数方程以及极坐标方程的应用,点到直线的距离的距离公式的应用,考查计算能力.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
12.已知二项式($\sqrt{x}$-$\frac{1}{x}$)n的展开式的第6项是常数项,则n的值是( )
| A. | 5 | B. | 8 | C. | 10 | D. | 15 |
15.定义运算a?b为执行如右图所示的程序框图输出的S值,则$({2^-}^{{{log}_2}3})?({log_{\frac{1}{2}}}4)$的值为( )
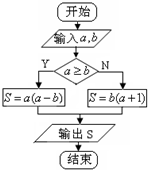

| A. | $\frac{7}{9}$ | B. | $-\frac{8}{3}$ | C. | 4 | D. | -4 |