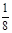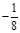题目内容
已知椭圆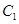 ,抛物线
,抛物线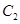 的焦点均在
的焦点均在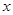 轴上,
轴上,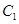 的中心和
的中心和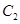 的顶点均为坐标原点
的顶点均为坐标原点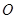 ,从每条曲线上各取两个点,将其坐标记录于表中:
,从每条曲线上各取两个点,将其坐标记录于表中:
(1)求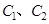 的标准方程;
的标准方程;
(2)请问是否存在直线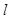 同时满足条件:(ⅰ)过
同时满足条件:(ⅰ)过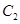 的焦点
的焦点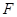 ;(ⅱ)与
;(ⅱ)与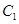 交于不同两点
交于不同两点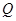 、
、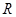 ,且满足
,且满足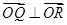 .若存在,求出直线
.若存在,求出直线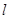 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
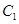 ,抛物线
,抛物线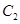 的焦点均在
的焦点均在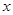 轴上,
轴上,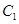 的中心和
的中心和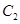 的顶点均为坐标原点
的顶点均为坐标原点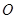 ,从每条曲线上各取两个点,将其坐标记录于表中:
,从每条曲线上各取两个点,将其坐标记录于表中: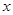 | 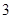 | 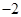 | 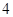 | 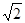 |
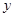 | 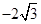 |  | 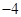 | 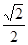 |
(1)求
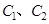 的标准方程;
的标准方程;(2)请问是否存在直线
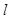 同时满足条件:(ⅰ)过
同时满足条件:(ⅰ)过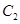 的焦点
的焦点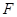 ;(ⅱ)与
;(ⅱ)与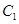 交于不同两点
交于不同两点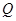 、
、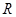 ,且满足
,且满足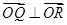 .若存在,求出直线
.若存在,求出直线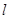 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.(Ⅰ)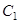 方程为
方程为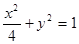
(Ⅱ)存在直线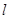 满足条件,且
满足条件,且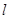 的方程为:
的方程为: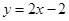 或
或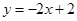
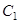 方程为
方程为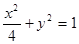
(Ⅱ)存在直线
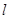 满足条件,且
满足条件,且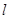 的方程为:
的方程为: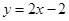 或
或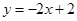
(1)设抛物线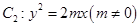 ,则有
,则有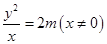 ,据此验证
,据此验证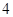 个点知
个点知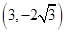 .
. 在抛物线上,易求
在抛物线上,易求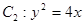 ,再设
,再设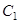 :
: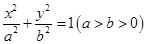 ,把点(
,把点(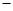 2,0)(
2,0)(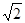 ,
,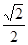 )代入得可建立关于a,b的两个方程,求出a,b值,从而得到椭圆方程.
)代入得可建立关于a,b的两个方程,求出a,b值,从而得到椭圆方程.
(II)由题意可知此直线斜率一定存在,从而可设直线l的方程为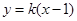 ,再与椭圆C1的方程联立消y后得关于x的一元二次方程,
,再与椭圆C1的方程联立消y后得关于x的一元二次方程,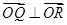 ,即
,即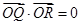 ,得
,得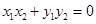 ,然后根据韦达定理可得到关于k的方程,求出k值,从而得到直线l的方程.
,然后根据韦达定理可得到关于k的方程,求出k值,从而得到直线l的方程.
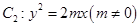 ,则有
,则有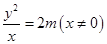 ,据此验证
,据此验证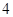 个点知
个点知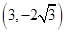 .
. 在抛物线上,易求
在抛物线上,易求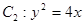 ,再设
,再设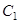 :
: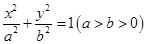 ,把点(
,把点(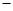 2,0)(
2,0)(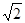 ,
,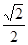 )代入得可建立关于a,b的两个方程,求出a,b值,从而得到椭圆方程.
)代入得可建立关于a,b的两个方程,求出a,b值,从而得到椭圆方程.(II)由题意可知此直线斜率一定存在,从而可设直线l的方程为
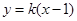 ,再与椭圆C1的方程联立消y后得关于x的一元二次方程,
,再与椭圆C1的方程联立消y后得关于x的一元二次方程,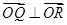 ,即
,即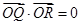 ,得
,得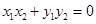 ,然后根据韦达定理可得到关于k的方程,求出k值,从而得到直线l的方程.
,然后根据韦达定理可得到关于k的方程,求出k值,从而得到直线l的方程.
练习册系列答案
相关题目
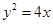 的焦点为
的焦点为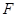 ,过点
,过点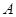 ,
,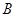 两点.
两点.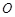 为坐标原点,求证:
为坐标原点,求证: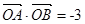 ;
;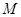 在线段
在线段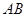 上运动,原点
上运动,原点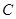 ,求四边形
,求四边形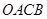 面积的最小值..
面积的最小值..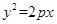 的焦点与
的焦点与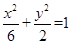 的左焦点重合,则
的左焦点重合,则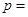 ( )
( )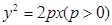 的焦点为
的焦点为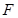 ,点
,点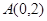 .若线段
.若线段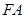 的中点
的中点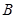 在抛物线上,则点
在抛物线上,则点 .
.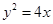 焦点的直线与抛物线交于
焦点的直线与抛物线交于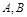 两点,
两点,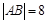 ,则线段
,则线段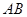 的中点横坐标为 。
的中点横坐标为 。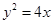 的焦点为
的焦点为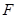 ,准线与
,准线与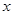 轴的交点为
轴的交点为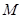 ,
,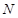 为抛物线上的一点,则满足
为抛物线上的一点,则满足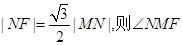 = 。
= 。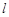 过抛物线
过抛物线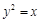 的焦点,且
的焦点,且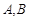 两点,若
两点,若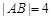 ,则弦
,则弦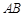 的中点到
的中点到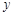 轴的距离为________
轴的距离为________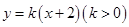 与抛物线
与抛物线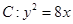 相交于
相交于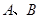 两点,
两点,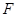 为
为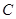 的焦点,若
的焦点,若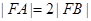 ,则
,则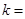
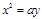 的准线方程是y=2,则实数a的值为( ).
的准线方程是y=2,则实数a的值为( ).