题目内容
设抛物线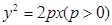 的焦点为
的焦点为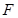 ,点
,点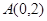 .若线段
.若线段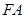 的中点
的中点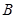 在抛物线上,则点
在抛物线上,则点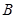 到该抛物线准线的距离为
到该抛物线准线的距离为 .
.
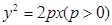 的焦点为
的焦点为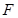 ,点
,点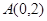 .若线段
.若线段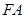 的中点
的中点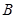 在抛物线上,则点
在抛物线上,则点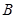 到该抛物线准线的距离为
到该抛物线准线的距离为 .
.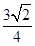
试题分析:因为抛物线的焦点
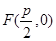 .则AF的中点
.则AF的中点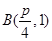 ,所以
,所以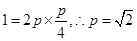 ,
,因而点B到抛物线准线:
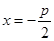 的距离为
的距离为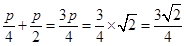 .
.点评:解本小题的突破口是求出F的坐标,再根据中点坐标公式求出B的坐标,利用点B在抛物线上,建立关于p的方程,得到p的值,从而得到点B到抛物线准线的距离.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
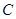 的顶点为原点,其焦点
的顶点为原点,其焦点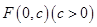 到直线
到直线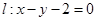 的距离为
的距离为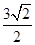 .设
.设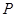 为直线
为直线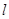 上的点,过点
上的点,过点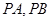 ,其中
,其中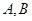 为切点.
为切点.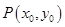 为直线
为直线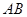 的方程;
的方程;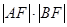 的最小值.
的最小值.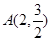 ,点
,点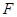 是抛物线
是抛物线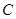 :
: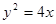 的焦点,点
的焦点,点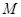 是抛物线
是抛物线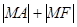 取最小值时点
取最小值时点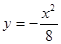 的焦点坐标为
的焦点坐标为 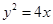 的准线方程是 .
的准线方程是 .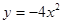 的焦点坐标是 .
的焦点坐标是 . 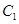 ,抛物线
,抛物线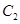 的焦点均在
的焦点均在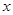 轴上,
轴上,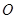 ,从每条曲线上各取两个点,将其坐标记录于表中:
,从每条曲线上各取两个点,将其坐标记录于表中: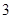
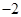
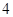
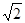
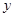
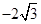

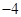
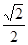
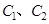 的标准方程;
的标准方程;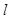 同时满足条件:(ⅰ)过
同时满足条件:(ⅰ)过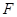 ;(ⅱ)与
;(ⅱ)与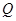 、
、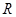 ,且满足
,且满足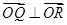 .若存在,求出直线
.若存在,求出直线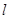 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.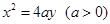 的焦点到其准线的距离为 .
的焦点到其准线的距离为 .