题目内容
【题目】已知函数![]() .
.
⑴当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
⑵若存在与函数![]() ,
,![]() 的图象都相切的直线,求实数
的图象都相切的直线,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,函数
时,函数![]() 取得极小值为
取得极小值为![]() ,无极大值;(2)
,无极大值;(2)![]()
【解析】试题分析:(1)![]() ,通过求导分析,得函数
,通过求导分析,得函数![]() 取得极小值为
取得极小值为![]() ,无极大值;(2)
,无极大值;(2)![]() ,所以
,所以![]() ,通过求导讨论,得到
,通过求导讨论,得到![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)函数![]() 的定义域为
的定义域为![]()
当![]() 时,
时,![]() ,
,
所以![]()
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以函数![]() 在区间
在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增,
单调递增,
所以当![]() 时,函数
时,函数![]() 取得极小值为
取得极小值为![]() ,无极大值;
,无极大值;
(2)设函数![]() 上点
上点![]() 与函数
与函数![]() 上点
上点![]() 处切线相同,
处切线相同,
则![]()
所以![]()
所以![]() ,代入
,代入![]() 得:
得:
![]()
设![]() ,则
,则![]()
不妨设![]() 则当
则当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
所以![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
代入![]() 可得:
可得:![]()
设![]() ,则
,则![]() 对
对![]() 恒成立,
恒成立,
所以![]() 在区间
在区间![]() 上单调递增,又
上单调递增,又![]()
所以当![]() 时
时![]() ,即当
,即当![]() 时
时![]() ,
,
又当![]() 时
时![]()
![]()
因此当![]() 时,函数
时,函数![]() 必有零点;即当
必有零点;即当![]() 时,必存在
时,必存在![]() 使得
使得![]() 成立;
成立;
即存在![]() 使得函数
使得函数![]() 上点
上点![]() 与函数
与函数![]() 上点
上点![]() 处切线相同.
处切线相同.
又由![]() 得:
得:![]()
所以![]() 单调递减,因此
单调递减,因此![]()
所以实数![]() 的取值范围是
的取值范围是![]() .
.

【题目】某中学为研究学生的身体素质与与课外体育锻炼时间的关系,对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查,如下表:(平均每天锻炼的时间单位:分钟)
将学生日均课外体育运动时间在![]() 上的学生评价为“课外体育达标”.
上的学生评价为“课外体育达标”.
平均每天锻炼的时间(分钟) |
|
|
|
|
|
|
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
请根据上述表格中的统计数据填写下面![]() 列联表,并通过计算判断是否能在犯错误的概率不超过
列联表,并通过计算判断是否能在犯错误的概率不超过![]() 的前提下认为“课外体育达标”与性别有关?
的前提下认为“课外体育达标”与性别有关?
课外体育不达标 | 课外体育达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
从上述200名学生中,按“课外体育达标”、“课外体育不达标”分层抽样,抽取4人得到一个样本,再从这个样本中抽取2人,求恰好抽到一名“课外体育不达标”学生的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】空气质量主要受污染物排放量及大气扩散等因素的影响,某市环保监测站2014年10月连续10天(从左到右对应1号至10号)采集该市某地平均风速及空气中氧化物的日均浓度数据,制成散点图如图所示.
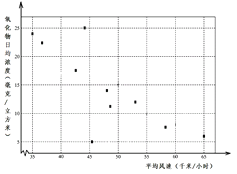
(Ⅰ)同学甲从这10天中随机抽取连续5天的一组数据,计算回归直线方程.试求连续5天的一组数据中恰好同时包含氧化物日均浓度最大与最小值的概率;
(Ⅱ)现有30名学生,每人任取5天数据,对应计算出30个不同的回归直线方程.已知30组数据中有包含氧化物日均浓度最值的有14组.现采用这30个回归方程对某一天平均风速下的氧化物日均浓度进行预测,若预测值与实测值差的绝对值小于2,则称之为“拟合效果好”,否则为“拟合效果不好”.根据以上信息完成下列2×2联表,并分析是否有95%以上的把握说拟合效果与选取数据是否包含氧化物日均浓度最值有关.
预测效果好 | 拟合效果不好 | 合计 | |
数据有包含最值 | 5 | ||
数据无包含最值 | 4 | ||
合计 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
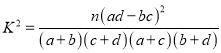 (其中
(其中![]() ).
).