ћвƒњƒЏ»Ё
°Њћвƒњ°њњ’∆ш÷ Ѕњ÷ч“™ №ќџ»Њќп≈≈Ј≈ЅњЉ∞іу∆шј©…Ґµ»“тЋЎµƒ”∞ѕм£ђƒ≥ –їЈ±£Ља≤в’Њ2014ƒк10‘¬Ѕђ–ш10ћм£®і”„уµљ”“ґ‘”¶1Ї≈÷Ѕ10Ї≈£©≤…ЉѓЄ√ –ƒ≥µЎ∆љЊщЈзЋўЉ∞њ’∆ш÷–—хїѓќпµƒ»’Њщ≈®ґ» эЊЁ£ђ÷∆≥……ҐµгЌЉ»зЌЉЋщ Њ£Ѓ
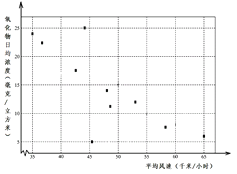
£®Ґс£©Ќђ—ІЉ„і”’в10ћм÷–Ћжїъ≥й»°Ѕђ–ш5ћмµƒ“ї„й эЊЁ£ђЉ∆ЋгїЎєй÷±ѕяЈљ≥ћ£Ѓ ‘«уЅђ–ш5ћмµƒ“ї„й эЊЁ÷–«°Ї√Ќђ ±∞ьЇђ—хїѓќп»’Њщ≈®ґ»„оіу”л„о–°÷µµƒЄ≈¬ £ї
£®Ґт£©ѕ÷”–30√ы—І…ъ£ђ√њ»Ћ»ќ»°5ћм эЊЁ£ђґ‘”¶Љ∆Ћг≥ц30Єц≤їЌђµƒїЎєй÷±ѕяЈљ≥ћ£Ѓ“—÷™30„й эЊЁ÷–”–∞ьЇђ—хїѓќп»’Њщ≈®ґ»„о÷µµƒ”–14„й£Ѓѕ÷≤…”√’в30ЄцїЎєйЈљ≥ћґ‘ƒ≥“їћм∆љЊщЈзЋўѕ¬µƒ—хїѓќп»’Њщ≈®ґ»љш––‘§≤в£ђ»ф‘§≤в÷µ”л µ≤в÷µ≤оµƒЊшґ‘÷µ–°”Џ2£ђ‘т≥∆÷Ѓќ™°∞ƒвЇѕ–ІєыЇ√°±£ђЈс‘тќ™°∞ƒвЇѕ–Ієы≤їЇ√°±£ЃЄщЊЁ“‘…ѕ–≈ѕҐЌк≥…ѕ¬Ѕ–2°Ѕ2Ѕ™±н£ђ≤ҐЈ÷ќц «Јс”–95%“‘…ѕµƒ∞—ќ’ЋµƒвЇѕ–Ієы”л—°»° эЊЁ «Јс∞ьЇђ—хїѓќп»’Њщ≈®ґ»„о÷µ”–єЎ£Ѓ
‘§≤в–ІєыЇ√ | ƒвЇѕ–Ієы≤їЇ√ | ЇѕЉ∆ | |
эЊЁ”–∞ьЇђ„о÷µ | 5 | ||
эЊЁќё∞ьЇђ„о÷µ | 4 | ||
ЇѕЉ∆ |
≤ќњЉ эЊЁ£Ї
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
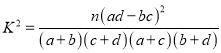 £®∆д÷–
£®∆д÷–![]() £©.
£©.
°Њір∞Є°њ£®1£©![]() £®2£©”–95%“‘…ѕµƒ∞—ќ’
£®2£©”–95%“‘…ѕµƒ∞—ќ’
°Њљвќц°њ ‘ћвЈ÷ќц£Ї£®1£©јы”√√ґЊўЈ®»Јґ®і”’в10ћм÷–Ћжїъ≥й»°“ї„йЅђ–ш5ћмµƒ эЊЁ∞ьЇђµƒїщ±Њ ¬Љю э£®6Єц£©£ђ‘ў»Јґ®°∞ эЊЁ÷–«°Ї√Ќђ ±∞ьЇђ—хїѓќп»’Њщ≈®ґ»„оіу”л„о–°÷µ°±∞ьЇђµƒїщ±Њ ¬Љю£®4Єц£©£ђ„оЇуЄщЊЁє≈µдЄ≈–ЌЄ≈¬ єЂ љ«уЄ≈¬ £®2£©ѕ»ЄщЊЁ…ҐµгЌЉ£ђћо–іѕа”¶ эЊЁ£ђ‘ўЄщЊЁєЂ љ«у![]() £ђ‘ўґ‘’’≤ќњЉ эЊЁ£ђ»Јґ®∞—ќ’–‘ґаіу.
£ђ‘ўґ‘’’≤ќњЉ эЊЁ£ђ»Јґ®∞—ќ’–‘ґаіу.
‘ћвљвќц£Ї£®Ґс£©Љ«µЏ![]() ћмЉа≤в эЊЁќ™
ћмЉа≤в эЊЁќ™![]() £®
£®![]() £©£ђ”…ЌЉѕу“„÷™
£©£ђ”…ЌЉѕу“„÷™![]() µƒ»’Њщ≈®ґ»„оіу£ђ
µƒ»’Њщ≈®ґ»„оіу£ђ ![]() µƒ»’Њщ≈®ґ»„о–°£Ѓі”’в10ћм÷–Ћжїъ≥й»°“ї„йЅђ–ш5ћмµƒ эЊЁ∞ьЇђµƒїщ±Њ ¬Љю”–£Ї
µƒ»’Њщ≈®ґ»„о–°£Ѓі”’в10ћм÷–Ћжїъ≥й»°“ї„йЅђ–ш5ћмµƒ эЊЁ∞ьЇђµƒїщ±Њ ¬Љю”–£Ї ![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £ђє≤6÷÷£Ѓ
£ђє≤6÷÷£Ѓ
Љ« ¬Љю![]() °∞ эЊЁ÷–«°Ї√Ќђ ±∞ьЇђ—хїѓќп»’Њщ≈®ґ»„оіу”л„о–°÷µ°±∞ьЇђµƒїщ±Њ ¬Љю”–£Ї
°∞ эЊЁ÷–«°Ї√Ќђ ±∞ьЇђ—хїѓќп»’Њщ≈®ґ»„оіу”л„о–°÷µ°±∞ьЇђµƒїщ±Њ ¬Љю”–£Ї ![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £ђє≤4÷÷£Ѓ
£ђє≤4÷÷£Ѓ
є Ѕђ–ш5ћмµƒ эЊЁ÷–«°Ї√Ќђ ±∞ьЇђ—хїѓќп»’Њщ≈®ґ»„о÷µµƒЄ≈¬ ![]() £Ѓ
£Ѓ
£®Ґт£©“јћв“в£ђЌк≥…2°Ѕ2Ѕ™±н»зѕ¬Ћщ Њ£Ѓ
‘§≤в„Љ»Ј | ‘§≤в≤ї„Љ»Ј | ЇѕЉ∆ | |
эЊЁ”–∞ьЇђ„о÷µ | 5 | 10 | 15 |
эЊЁ√ї”–∞ьЇђ„о÷µ | 11 | 4 | 15 |
ЇѕЉ∆ | 16 | 14 | 30 |
”…єЂ љ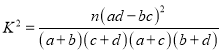 £ђЉ∆Ћгµ√
£ђЉ∆Ћгµ√![]() £Ѓ
£Ѓ
”…≤ќњЉ эЊЁњ…÷™£ђ ![]() £ђє ”–95%“‘…ѕµƒ∞—ќ’ЋµƒвЇѕ–Ієы”л—°»° эЊЁ «Јс∞ьЇђ—хїѓќп»’Њщ≈®ґ»„о÷µ”–єЎ£Ѓ
£ђє ”–95%“‘…ѕµƒ∞—ќ’ЋµƒвЇѕ–Ієы”л—°»° эЊЁ «Јс∞ьЇђ—хїѓќп»’Њщ≈®ґ»„о÷µ”–єЎ£Ѓ

 љћ≤ƒ»Ђљв„÷і Њд∆™ѕµЅ–ір∞Є
љћ≤ƒ»Ђљв„÷і Њд∆™ѕµЅ–ір∞Є