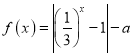Question

【题目】已知椭圆C的焦点为(，0)，(，0)，且椭圆C过点M(4，1)，直线l：不过点M，且与椭圆交于不同的两点A，B．

（1）求椭圆C的标准方程；

（2）求证：直线MA，MB与x轴总围成一个等腰三角形．

Answer 1

【答案】（1）（2）详见解析

【解析】

（1）利用椭圆的定义先求出2a的值，可得出的值，再利用a、b、c之间的关系求出b的值，从而得出椭圆C的标准方程；

（2）将直线l的方程与椭圆C的方程联立，列出韦达定理，利用斜率公式以及韦达定理计算出直线MA、MB的斜率互为相反数来证明结论成立．

（1）设椭圆的方程为，则，解得，

所以椭圆的标准方程为.

（2）将代入并整理得，

则，.

∵直线：与椭圆交于不同的两点，，∴，解得，

∴直线，的斜率存在且不为零.

设直线，的斜率分别为和，只要证明.

设，，

.

故原命题成立.