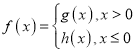题目内容
【题目】已知函数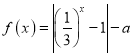 .
.
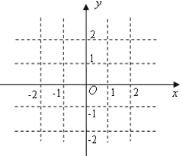
(1)若![]() ,画出函数
,画出函数![]() 的图象,并指出函数的单调区间;
的图象,并指出函数的单调区间;
(2)讨论函数![]() 的零点个数.
的零点个数.
【答案】(1)图象见解析;增区间为![]() ,减区间为
,减区间为![]() (2)见解析.
(2)见解析.
【解析】
(1)将![]() 代入函数
代入函数![]() 的表达式,并将该函数表示为分段函数,利用翻折变换可得出函数
的表达式,并将该函数表示为分段函数,利用翻折变换可得出函数![]() 的图象,并利用图象得出该函数的增区间和减区间;
的图象,并利用图象得出该函数的增区间和减区间;
(2)令![]() ,得
,得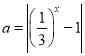 ,则函数
,则函数![]() 的零点个数转化为直线
的零点个数转化为直线![]() 与函数
与函数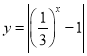 的交点个数,结合(1)中的图象,可得出实数
的交点个数,结合(1)中的图象,可得出实数![]() 在不同取值下函数
在不同取值下函数![]() 的零点个数.
的零点个数.
(1)当![]() 时,
时,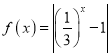 .
.
令![]() ,即
,即![]() ,得
,得![]() ;
;
令![]() ,即
,即![]() ,得
,得![]() .
.
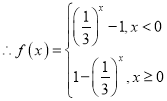 ,函数
,函数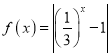 的图象如下图所示:
的图象如下图所示:
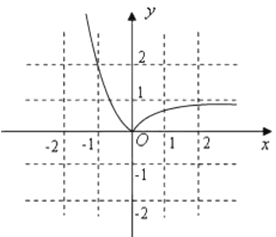
由图象可知,函数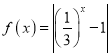 单调减区间为
单调减区间为![]() ,增区间为
,增区间为![]() ;
;
(2)令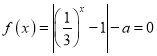 ,得
,得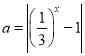 ,则函数
,则函数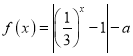 的零点个数等价于直线
的零点个数等价于直线![]() 与函数
与函数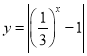 图象的交点个数.
图象的交点个数.
如上图所示,当![]() 时,函数
时,函数![]() 的零点个数为
的零点个数为![]() ;
;
当![]() 或
或![]() 时,函数
时,函数![]() 的零点个数为
的零点个数为![]() ;
;
当![]() 时,函数
时,函数![]() 的零点个数为
的零点个数为![]() .
.

练习册系列答案
相关题目