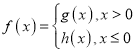Question

【题目】已知函数，其中e是自然数对数的底数，若，则实数a的取值范围是( )

A. B. C. D.

Answer 1

【答案】B

【解析】

利用函数的奇偶性将函数转化为f（M）≤f（N）的形式，再利用单调性脱去对应法则f，转化为一般的二次不等式求解即可．

由于，，则f（﹣x）＝﹣x3+e﹣x﹣ex＝﹣f（x），故函数f（x）为奇函数．

故原不等式f（a﹣1）+f（2a2）≤0，可转化为f（2a2）≤﹣f（a﹣1）＝f（1﹣a），即f（2a2）≤f（1﹣a）；

又f'（x）＝3x2﹣cosx+ex+e﹣x，由于ex+e﹣x≥2，故ex+e﹣x﹣cosx>0，

所以f'（x）＝3x2﹣cosx+ex+e﹣x≥0恒成立，

故函数f（x）单调递增，则由f（2a2）≤f（1﹣a）可得，2a2≤1﹣a，即2a2+a﹣1≤0，

解得，

故选：B．