题目内容
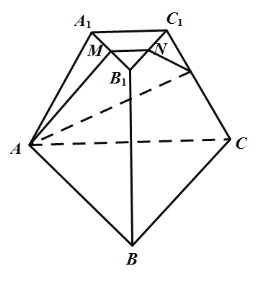
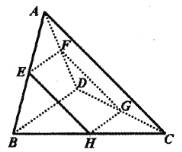
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,H为PC的中点,M为AH中点,PA=AC=2,BC=1.
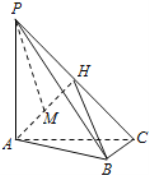
(Ⅰ)求证:AH⊥平面PBC;
(Ⅱ)求PM与平面AHB成角的正弦值;
(Ⅲ)在线段PB上是否存在点N,使得MN∥平面ABC,若存在,请说明点N的位置,若不存在,请说明理由.
【答案】(Ⅰ)见证明;(Ⅱ)![]() (Ⅲ)点N是靠近B点的四等分点
(Ⅲ)点N是靠近B点的四等分点
【解析】
(Ⅰ)根据线面垂直判定与性质定理进行论证,(Ⅱ)先根据条件建立空间直角坐标系,设立各点坐标,列方程组解得平面AHB的一个法向量,根据向量数量积求向量夹角,最后根据向量夹角与线面角关系得结果,(Ⅲ)先设N坐标,再根据![]() 与平面ABC的法向量的数量积为零解得结果.
与平面ABC的法向量的数量积为零解得结果.
(Ⅰ)证明:∵PA⊥底面ABC,
∴PA⊥BC,
又∵AC⊥BC,PA∩AC=A,
∴BC⊥平面PAC,
∵AH平面PAC,
∴BC⊥AH.
∵H为PC的中点,PA=AC,
∴AH⊥PC.
∵PC∩BC=C.
∴AH⊥平面PBC;
(Ⅱ)
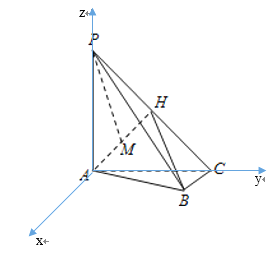
由题意建立空间直角坐标系.A(0,0,0),B(1,2,0),C(0,2,0),
P(0,0,2),H(0,1,1),M![]() .
.
![]() =(0,1,1),
=(0,1,1),![]() =(1,2,0),
=(1,2,0),![]() =
=![]() .
.
设平面ABH的法向量为![]() =(x,y,z),则
=(x,y,z),则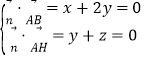 ,取
,取![]() =(2,-1,1).
=(2,-1,1).
设PM与平面AHB成角为![]() ,
,
则sin![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
所以PM与平面AHB成角的正弦值为![]()
(Ⅲ)假设在线段PB上存在点N,使得MN∥平面ABC.
设![]() ,
,![]() =(1,2,-2),
=(1,2,-2),
∴![]() .
.
∴![]() =
=![]() =
=![]() ,
,
∵MN∥平面ABC,平面ABC的法向量为![]() =(0,0,2),
=(0,0,2),
∴![]() =
=![]() -
-![]() =0,解得
=0,解得![]() .
.
∴点N是靠近B点的四等分点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目