题目内容
已知函数y=f(x)=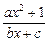 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)< .
.
(1)试求函数f(x)的解析式;
(2)问函数f(x)图象上是否存在关于点(1,0)对称的两点,若存在,求出点的坐标;若不存在,说明理由.
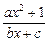 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)< .
.(1)试求函数f(x)的解析式;
(2)问函数f(x)图象上是否存在关于点(1,0)对称的两点,若存在,求出点的坐标;若不存在,说明理由.
(1) f(x)=x+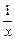 , (2) y=f(x)图象上存在两点(1+
, (2) y=f(x)图象上存在两点(1+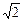 ,2
,2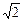 ),(1-
),(1-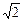 ,-2
,-2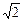 )关于(1,0)对称
)关于(1,0)对称
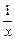 , (2) y=f(x)图象上存在两点(1+
, (2) y=f(x)图象上存在两点(1+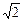 ,2
,2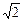 ),(1-
),(1-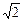 ,-2
,-2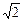 )关于(1,0)对称
)关于(1,0)对称(1)∵f(x)是奇函数,
∴f(-x)=-f(x),即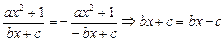
∴c=0,∵a>0,b>0,x>0,∴f(x)=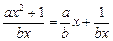 ≥2
≥2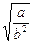 ,
,
当且仅当x=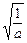 时等号成立,于是2
时等号成立,于是2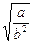 =2,∴a=b2,
=2,∴a=b2,
由f(1)< 得
得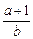 <
< 即
即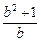 <
< ,∴2b2-5b+2<0,解得
,∴2b2-5b+2<0,解得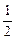 <b<2,又b∈N,∴b=1,∴a=1,∴f(x)=x+
<b<2,又b∈N,∴b=1,∴a=1,∴f(x)=x+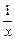 .
.
(2)设存在一点(x0,y0)在y=f(x)的图象上,并且关于(1,0)的对称点(2-x0,-y0)也在y=f(x)图象上,则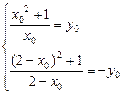
消去y0得x02-2x0-1=0,x0=1±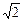 .
.
∴y=f(x)图象上存在两点(1+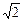 ,2
,2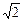 ),(1-
),(1-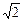 ,-2
,-2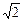 )关于(1,0)对称.
)关于(1,0)对称.
∴f(-x)=-f(x),即
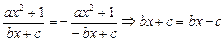
∴c=0,∵a>0,b>0,x>0,∴f(x)=
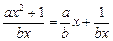 ≥2
≥2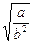 ,
,当且仅当x=
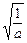 时等号成立,于是2
时等号成立,于是2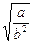 =2,∴a=b2,
=2,∴a=b2, 由f(1)<
 得
得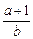 <
< 即
即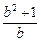 <
< ,∴2b2-5b+2<0,解得
,∴2b2-5b+2<0,解得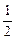 <b<2,又b∈N,∴b=1,∴a=1,∴f(x)=x+
<b<2,又b∈N,∴b=1,∴a=1,∴f(x)=x+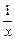 .
. (2)设存在一点(x0,y0)在y=f(x)的图象上,并且关于(1,0)的对称点(2-x0,-y0)也在y=f(x)图象上,则
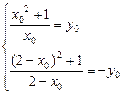
消去y0得x02-2x0-1=0,x0=1±
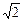 .
. ∴y=f(x)图象上存在两点(1+
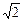 ,2
,2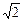 ),(1-
),(1-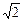 ,-2
,-2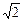 )关于(1,0)对称.
)关于(1,0)对称. 
练习册系列答案
相关题目
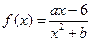 的图像在点
的图像在点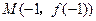 处的切线方程为
处的切线方程为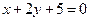 .
.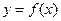 的解析式; (Ⅱ)求函数
的解析式; (Ⅱ)求函数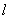 上,
上,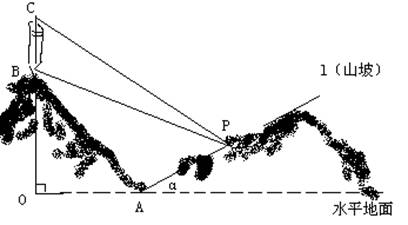
 设函数
设函数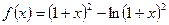 .
.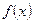 的单调区间;
的单调区间;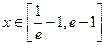 时,不等式
时,不等式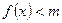 恒成立,求实数
恒成立,求实数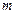 的取值范围;
的取值范围;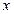 的方程
的方程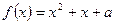 在
在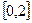 上恰有两个相异实根,求
上恰有两个相异实根,求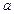 的取值范围.
的取值范围. =x.
=x. 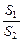 的解析式并求f(x)的定义域.
的解析式并求f(x)的定义域. 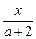 =|a-1|+2的根的取值范围.
=|a-1|+2的根的取值范围.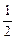 ,
,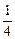 )的切线的倾斜角是
)的切线的倾斜角是