题目内容
某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔高BC=80(米),塔所在的山高OB=220(米),OA=200(米),图中所示的山坡可视为直线l且点P在直线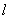 上,
上,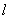 与水平地面的夹角为a ,tana=1/2试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)
与水平地面的夹角为a ,tana=1/2试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)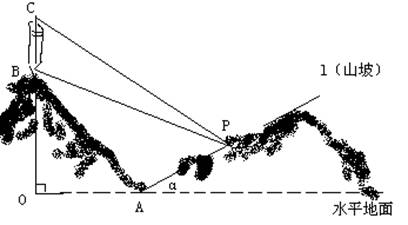
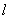 上,
上, 与水平地面的夹角为a ,tana=1/2试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)
与水平地面的夹角为a ,tana=1/2试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)
如图所示,建立平面直角坐标系,
则A(200,0),B(0,220),C(0,300),
直线l的方程为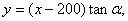 即
即
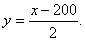 设点P的坐标为(x,y),
设点P的坐标为(x,y),
则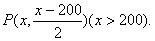
由经过两点的直线的斜率公式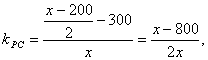
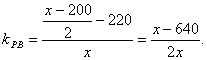
由直线PC到直线PB的角的公式得
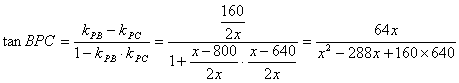
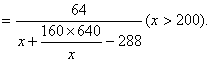
要使tanBPC达到最大,只须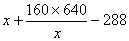 达到最小,由均值不等式
达到最小,由均值不等式
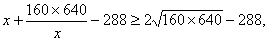
当且仅当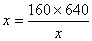 时上式取得等号,故当x=320时tanBPC最大,这时,点P的纵坐标y为
时上式取得等号,故当x=320时tanBPC最大,这时,点P的纵坐标y为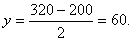
由此实际问题知,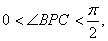 所以tanBPC最大时,∠BPC最大,故当此人距水平地面60米高时,观看铁塔的视角∠BPC最大。
所以tanBPC最大时,∠BPC最大,故当此人距水平地面60米高时,观看铁塔的视角∠BPC最大。
则A(200,0),B(0,220),C(0,300),
直线l的方程为
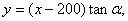 即
即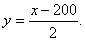 设点P的坐标为(x,y),
设点P的坐标为(x,y),则
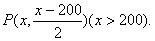
由经过两点的直线的斜率公式
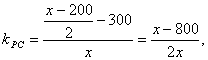
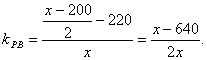
由直线PC到直线PB的角的公式得
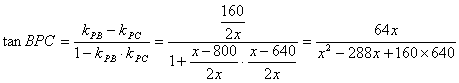
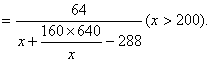
要使tanBPC达到最大,只须
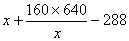 达到最小,由均值不等式
达到最小,由均值不等式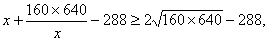
当且仅当
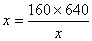 时上式取得等号,故当x=320时tanBPC最大,这时,点P的纵坐标y为
时上式取得等号,故当x=320时tanBPC最大,这时,点P的纵坐标y为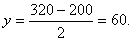
由此实际问题知,
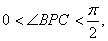 所以tanBPC最大时,∠BPC最大,故当此人距水平地面60米高时,观看铁塔的视角∠BPC最大。
所以tanBPC最大时,∠BPC最大,故当此人距水平地面60米高时,观看铁塔的视角∠BPC最大。本小题考查根据实际问题建立函数关系并应用解析几何和代数的方法解决实际问题的能力。

练习册系列答案
相关题目
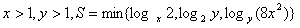 则S的最大值为 。
则S的最大值为 。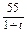 (单位:m/s)紧急刹车至停止.求:
(单位:m/s)紧急刹车至停止.求: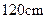 的正方形铁皮做一个无盖水箱,先在四角分别截去一个小正方形,然后把四边翻转
的正方形铁皮做一个无盖水箱,先在四角分别截去一个小正方形,然后把四边翻转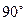 角,再焊接成水箱.问:水箱底边的长取多少时,水箱容积最大?最大容积是多少?
角,再焊接成水箱.问:水箱底边的长取多少时,水箱容积最大?最大容积是多少?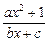 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)< .
.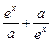 是R上的偶函数,(1)求a的值;(2)证明: f(x)在(0,+∞)上是增函数.
是R上的偶函数,(1)求a的值;(2)证明: f(x)在(0,+∞)上是增函数. 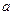 的正三角形的厚纸,从这块厚纸的三个角,按右图那样切下三个全等的四边形后,做成一个无盖的盒子,要使这个盒子容积最大,
的正三角形的厚纸,从这块厚纸的三个角,按右图那样切下三个全等的四边形后,做成一个无盖的盒子,要使这个盒子容积最大, 值应为多少?
值应为多少?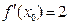 ,则
,则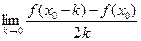 等于( )
等于( )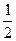
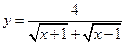 的导数.
的导数.