题目内容
已知曲线C1:y=x2与C2:y=-(x-2)2,直线l与C1、C2都相切,求直线l的方程.
y=0或y=4x-4
利用解方程组求交点,利用直线间的位置和待定系数法求斜率.
设l与C1相切于点P(x1,x12),与C2相切于Q(x2,-(x2-2)2)
对于C1:y′=2x,则与C1相切于点P的切线方程为
y-x12=2x1(x-x1),即y=2x1x-x12 ①
对于C2:y′=-2(x-2),与C2相切于点Q的切线方程为y+(x2-2)2=-2(x2-2)(x-x2),即y=-2(x2-2)x+x22-4 ②
∵两切线重合,∴2x1=-2(x2-2)且-x12=x22-4,解得x1=0,x2=2或x1=2,x2=0
∴直线l方程为y=0或y=4x-4
设l与C1相切于点P(x1,x12),与C2相切于Q(x2,-(x2-2)2)
对于C1:y′=2x,则与C1相切于点P的切线方程为
y-x12=2x1(x-x1),即y=2x1x-x12 ①
对于C2:y′=-2(x-2),与C2相切于点Q的切线方程为y+(x2-2)2=-2(x2-2)(x-x2),即y=-2(x2-2)x+x22-4 ②
∵两切线重合,∴2x1=-2(x2-2)且-x12=x22-4,解得x1=0,x2=2或x1=2,x2=0
∴直线l方程为y=0或y=4x-4

练习册系列答案
相关题目
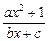 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<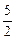 .
.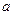 的正三角形的厚纸,从这块厚纸的三个角,按右图那样切下三个全等的四边形后,做成一个无盖的盒子,要使这个盒子容积最大,
的正三角形的厚纸,从这块厚纸的三个角,按右图那样切下三个全等的四边形后,做成一个无盖的盒子,要使这个盒子容积最大,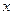 值应为多少?
值应为多少? 在点
在点 和
和 处的切线方程。
处的切线方程。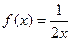 在
在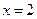 处的导数。
处的导数。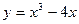 在点
在点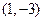 处的切线倾斜角为__________;
处的切线倾斜角为__________;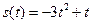 ,其初速度为( )
,其初速度为( )