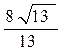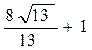题目内容
14分)如图,半圆O的半径为2,A为直径延长线上的一点,且OA=4,B为半圆周上任意一点,从AB向外作等边 ,设
,设 ,(1)将AB的长用
,(1)将AB的长用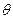 表示,(2)将四边形OACB的面积用
表示,(2)将四边形OACB的面积用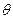 表示,(3)问当
表示,(3)问当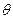 为何值时,四边形OACB的面积最大?最大面积是多少?
为何值时,四边形OACB的面积最大?最大面积是多少?
 ,设
,设 ,(1)将AB的长用
,(1)将AB的长用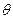 表示,(2)将四边形OACB的面积用
表示,(2)将四边形OACB的面积用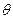 表示,(3)问当
表示,(3)问当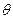 为何值时,四边形OACB的面积最大?最大面积是多少?
为何值时,四边形OACB的面积最大?最大面积是多少?
1)AB2=22+42-2×2×4cosθ=20-16cosθ2)8 sin(θ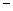
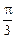 )+5
)+5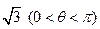 3)
3) 时Smax=8+5
时Smax=8+5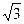
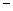
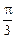 )+5
)+5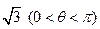 3)
3) 时Smax=8+5
时Smax=8+5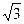
解:(1)AB2=22+42-2×2×4cosθ="20-16cosθ, "
故AB="… " …….. 4分
(2) SOACB=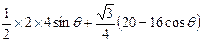 =4sinθ-4
=4sinθ-4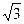 cosθ+ 5
cosθ+ 5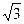
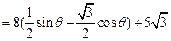 ="8" sin(θ
="8" sin(θ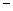
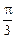 )+5
)+5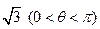 … 10分
… 10分
(3) ∴当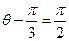 ,即
,即 时Smax=8+5
时Smax=8+5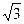 … 14分
… 14分
故AB="… " …….. 4分
(2) SOACB=
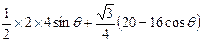 =4sinθ-4
=4sinθ-4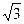 cosθ+ 5
cosθ+ 5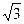
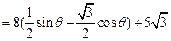 ="8" sin(θ
="8" sin(θ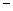
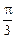 )+5
)+5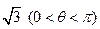 … 10分
… 10分(3) ∴当
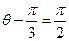 ,即
,即 时Smax=8+5
时Smax=8+5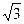 … 14分
… 14分
练习册系列答案
相关题目
 为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点。
为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点。 ,求圆C的方程;
,求圆C的方程; 的最小值及此时点P的坐标。
的最小值及此时点P的坐标。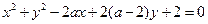 ,其中
,其中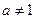 ,且
,且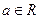 .
.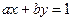 与圆
与圆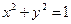 相交于
相交于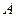 、
、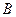 两点(其中
两点(其中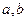 是实数),且
是实数),且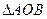 是直角三角形
是直角三角形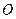 是坐标原点),则点
是坐标原点),则点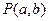 与点
与点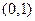 之间距离的最大值为 ▲ ;
之间距离的最大值为 ▲ ;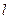 过点
过点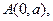 斜率为1,圆
斜率为1,圆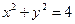 上恰有1个点到
上恰有1个点到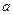 的值为( )
的值为( )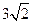

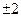
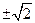
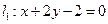 与直线
与直线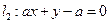 交于点
交于点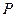 ,
,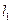 与
与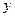 轴交于点
轴交于点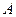 ,
,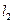 与
与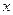 轴交于点
轴交于点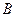 ,若
,若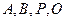 四点在同一圆周上(其中
四点在同一圆周上(其中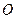 为坐标原点),则实数
为坐标原点),则实数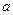 的值是( )
的值是( )



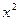 +
+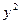 -4
-4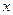 +3=0上的动点,则点P到直线
+3=0上的动点,则点P到直线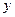 +1=0的距离的
+1=0的距离的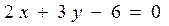 上运动,另一点B在圆
上运动,另一点B在圆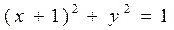 上运动,则|AB|的最小值是
上运动,则|AB|的最小值是