题目内容
(本小题满分15分)
已知以点 为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点。
为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点。
(Ⅰ)求证:△AOB的面积为定值;
(Ⅱ)设直线2x+y-4=0与圆C交于点M、N,若 ,求圆C的方程;
,求圆C的方程;
(Ⅲ)在(Ⅱ)的条件下,设P、Q分别是直线l:x+y+2=0和圆C的动点,求 的最小值及此时点P的坐标。
的最小值及此时点P的坐标。
已知以点
 为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点。
为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点。(Ⅰ)求证:△AOB的面积为定值;
(Ⅱ)设直线2x+y-4=0与圆C交于点M、N,若
 ,求圆C的方程;
,求圆C的方程;(Ⅲ)在(Ⅱ)的条件下,设P、Q分别是直线l:x+y+2=0和圆C的动点,求
 的最小值及此时点P的坐标。
的最小值及此时点P的坐标。(Ⅰ)略
(Ⅱ)圆C的方程为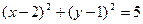
(Ⅲ) 的最小值为
的最小值为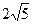 ,直线
,直线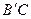 的方程为
的方程为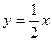 ,则直线
,则直线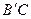 与直线x+y+2=0的交点P的坐标为
与直线x+y+2=0的交点P的坐标为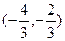
(Ⅱ)圆C的方程为
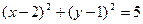
(Ⅲ)
 的最小值为
的最小值为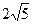 ,直线
,直线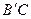 的方程为
的方程为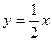 ,则直线
,则直线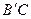 与直线x+y+2=0的交点P的坐标为
与直线x+y+2=0的交点P的坐标为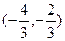
解:(Ⅰ)由题设知,圆C的方程为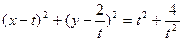 ,化简得
,化简得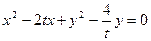 ,当y=0时,x=0或2t,则
,当y=0时,x=0或2t,则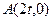 ;当x=0时,y=0或
;当x=0时,y=0或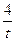 ,则
,则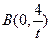 ,
,
∴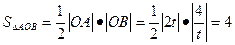 为定值。 ……………5分
为定值。 ……………5分
(II)∵ ,则原点O在MN的中垂线上,设MN的中点为H,则CH⊥MN,∴C、H、O三点共线,则直线OC的斜率
,则原点O在MN的中垂线上,设MN的中点为H,则CH⊥MN,∴C、H、O三点共线,则直线OC的斜率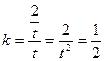 ,∴t=2或t=-2
,∴t=2或t=-2
∴圆心C(2,1)或C(-2,-1)∴圆C的方程为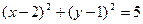 或
或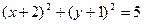 ,由于当圆方程为
,由于当圆方程为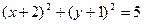 时,直线2x+y-4=0到圆心的距离d>r,此时不满足直线与圆相交,故舍去。
时,直线2x+y-4=0到圆心的距离d>r,此时不满足直线与圆相交,故舍去。
∴圆C的方程为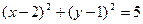 ……………10分
……………10分
(Ⅲ)点B(0,2)关于直线x+y+2=0的对称点为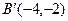 ,则
,则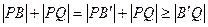 ,又
,又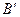 到圆上点Q的最短距离为
到圆上点Q的最短距离为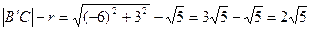 。
。
所以 的最小值为
的最小值为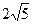 ,直线
,直线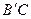 的方程为
的方程为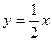 ,则直线
,则直线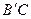 与直线x+y+2=0的交点P的坐标为
与直线x+y+2=0的交点P的坐标为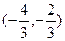 ……………15分
……………15分
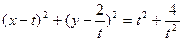 ,化简得
,化简得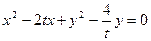 ,当y=0时,x=0或2t,则
,当y=0时,x=0或2t,则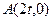 ;当x=0时,y=0或
;当x=0时,y=0或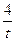 ,则
,则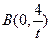 ,
,∴
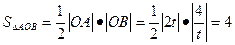 为定值。 ……………5分
为定值。 ……………5分(II)∵
 ,则原点O在MN的中垂线上,设MN的中点为H,则CH⊥MN,∴C、H、O三点共线,则直线OC的斜率
,则原点O在MN的中垂线上,设MN的中点为H,则CH⊥MN,∴C、H、O三点共线,则直线OC的斜率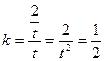 ,∴t=2或t=-2
,∴t=2或t=-2∴圆心C(2,1)或C(-2,-1)∴圆C的方程为
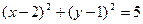 或
或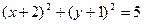 ,由于当圆方程为
,由于当圆方程为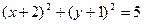 时,直线2x+y-4=0到圆心的距离d>r,此时不满足直线与圆相交,故舍去。
时,直线2x+y-4=0到圆心的距离d>r,此时不满足直线与圆相交,故舍去。∴圆C的方程为
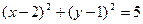 ……………10分
……………10分(Ⅲ)点B(0,2)关于直线x+y+2=0的对称点为
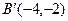 ,则
,则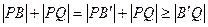 ,又
,又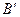 到圆上点Q的最短距离为
到圆上点Q的最短距离为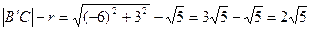 。
。所以
 的最小值为
的最小值为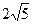 ,直线
,直线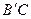 的方程为
的方程为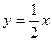 ,则直线
,则直线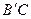 与直线x+y+2=0的交点P的坐标为
与直线x+y+2=0的交点P的坐标为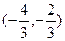 ……………15分
……………15分
练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 经过
经过 、
、 两点,且圆心在直线
两点,且圆心在直线 上.
上.  经过点
经过点 且与圆
且与圆 ,设
,设 ,(1)将AB的长用
,(1)将AB的长用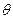 表示,(2)将四边形OACB的面积用
表示,(2)将四边形OACB的面积用
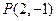 为圆
为圆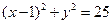 的弦
的弦 的中点,则直线
的中点,则直线



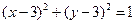 上或圆内的任意一点,O为坐标原点,
上或圆内的任意一点,O为坐标原点,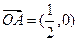 ,则
,则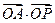 的最小值为( )
的最小值为( )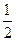
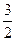
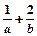 的最小值是________.
的最小值是________. 和圆:
和圆: 交于
交于 两点,
两点, 的垂直平分线的方程是( )
的垂直平分线的方程是( )



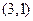 作直线与圆
作直线与圆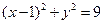 相交于M、N两点,则
相交于M、N两点,则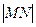 的最小值为( )
的最小值为( )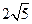
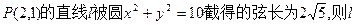 的方程为 。
的方程为 。