题目内容
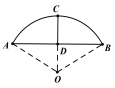
【题目】已知三棱柱
中,三个侧面均为矩形,底面
为等腰直角三角形, 
,点
为棱
的中点,点
在棱
上运动.
（1）求证
；
（2）当点运动到某一位置时，恰好使二面角
的平面角的余弦值为
，求点到平面
的距离；
（3）在（2）的条件下，试确定线段
上是否存在一点
，使得
平面
？若存在，确定其位置；若不存在，说明理由.
【答案】（1）见解析；（2）
；（3）存在，为
中点.
【解析】
（1）以CB为x轴，CA为y轴，CC1为z轴，C为原点建立坐标系，设E（m，0，2），要证A1C⊥AE，可证
,只需证明
，利用向量的数量积运算即可证明；（2）分别求出平面EA1D、平面A1DB的一个法向量，由两法向量夹角余弦值的绝对值等于
，解得m值，由此可得答案；（3）在（2）的条件下，设F（x，y，0），可知
与平面A1DB的一个法向量平行，由此可求出点F坐标，进而求出||，即得答案.
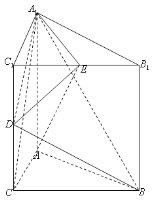
（1）以CB为x轴，CA为y轴，CC1为z轴，C为原点建立坐标系，设E（m，0，2），
C（0，0，0），A（0，2，0），A1（0，2，2），D（0，0，1），B（2，0，0），
＝（0，﹣2，﹣2），
＝（m，﹣2，2），
因为
＝0+（﹣2）×（﹣2）﹣2×2＝0，
所以⊥，即A1C⊥AE；
（2）
＝（m，0，1），
＝（0，2，1），
设
＝（x，y，z）为平面EA1D的一个法向量，
则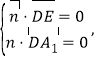
即
，取＝（2，m，﹣2m），
＝（2，0，﹣1），设＝（x，y，z）为平面A1DB的一个法向量，
则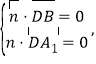
，即
，取＝（1，﹣1，2），
由二面角E﹣A1D﹣B的平面角的余弦值为 ，得
||＝，解得m＝1，
平面A1DB的一个法向量＝（1，﹣1，2），根据点E到面的距离为：
.
（3）由（2）知E（1，0，2），且＝（1，﹣1，2）为平面A1DB的一个法向量，
设F（x，y，0），则
＝（x﹣1，y，﹣2），且
，所以x﹣1＝﹣1，y＝1，解得x＝0，y＝1，
所以＝（﹣1，1，﹣2），
＝
＝
，
故EF的长度为，此时点F（0，1，0）．存在F点为AC中点.
