题目内容
【题目】已知函数f(x)=ln(x+1)-mx(m![]() R)。(1)若m>0,讨论f(x)的单调性;(2)令g(x)=f(x-1)+(2m+1)x+n,若g(x)有两个零点
R)。(1)若m>0,讨论f(x)的单调性;(2)令g(x)=f(x-1)+(2m+1)x+n,若g(x)有两个零点![]() ,
,![]() ,求证:
,求证: ![]() <
<![]()
【答案】(1)单调增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)见解析
;(2)见解析
【解析】试题分析:
(1)求出导函数,根据导函数的符号判断出函数的单调性即可.(2)由![]() 两式相减后整理可得
两式相减后整理可得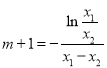 .故要证不等式成立,只需证
.故要证不等式成立,只需证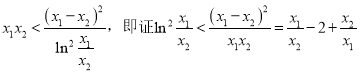 .不妨设
.不妨设![]() ,
, ![]() ,则只需证
,则只需证![]() ,然后再构造函数
,然后再构造函数![]() ,证明
,证明![]() 即可.
即可.
试题解析:
(1)∵![]() ,
,
∴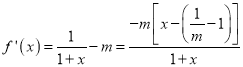 ,
,
∵![]() ,
,
∴![]() .
.
当![]() 时,
时, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() 单调递减.
单调递减.
∴函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
(2)由题意得![]() ,
,
∵函数g(x)有两个零点![]() ,
,
∴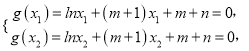
两式相减得![]()
∴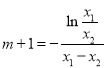 ,
,
要证![]() ,即证
,即证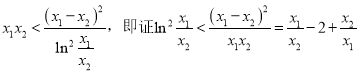 ,
,
不妨设![]() ,
, ![]() ,
,
则只需证![]() .
.
令![]() ,
,
则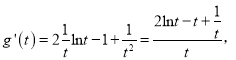
令![]() ,
,
则![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,
,
∴函数![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
即![]() 在
在![]() 上恒成立,故原不等式成立.
上恒成立,故原不等式成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
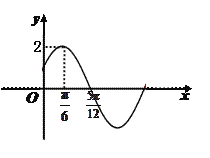
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并求出函数![]() 的解析式;
的解析式;
(2)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.