Question

【题目】已知椭圆与直线y=x-2相切，设椭圆的上顶点为M， 是椭圆的左右焦点，且⊿M为等腰直角三角形。（1）求椭圆的标准方程；（2）直线l过点N（0，-）交椭圆于A，B两点，直线MA、MB分别与椭圆的短轴为直径的圆交于S，T两点，求证：O、S、T三点共线。

Answer 1

【答案】（1）；（2）见解析

【解析】试题分析：

（1）由为等腰直角三角形可得，再由直线和椭圆相切并根据判别式可得，于是可得椭圆的方程．（2）由题意要证O、S、T三点共线，只需证明ST为圆的直径即可，根据题意只需证明，通过计算得到即可．

试题解析：

（1）解：∵为等腰直角三角形，

∴，

∴椭圆的方程为．

由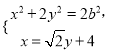消去x整理得 ，

∵椭圆与直线相切，

∴

解得．

∴椭圆的标准方程为，即．

（2）证明：由题意得直线AB的斜率存在，设直线的方程为，

由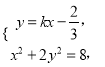消去y整理得，

∵直线AB与椭圆交于两点，

∴．

设点，

则，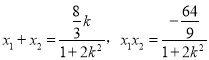

又，

∴，

．

∴，

∴，

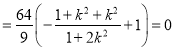又圆的直径为椭圆的短轴，故圆心为原点，

∴点三点共线．