题目内容
设函数f(x)=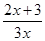 (x>0),数列{an}满足a1=1,an=f
(x>0),数列{an}满足a1=1,an=f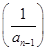 (n∈N*,且n≥2).
(n∈N*,且n≥2).
(1)求数列{an}的通项公式;
(2)设Tn=a1a2-a2a3+a3a4-a4a5+…+(-1)n-1·anan+1,若Tn≥tn2对n∈N*恒成立,求实数t的取值范围.
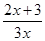 (x>0),数列{an}满足a1=1,an=f
(x>0),数列{an}满足a1=1,an=f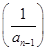 (n∈N*,且n≥2).
(n∈N*,且n≥2).(1)求数列{an}的通项公式;
(2)设Tn=a1a2-a2a3+a3a4-a4a5+…+(-1)n-1·anan+1,若Tn≥tn2对n∈N*恒成立,求实数t的取值范围.
(1)an=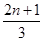 (2)
(2)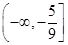
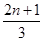 (2)
(2)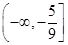
(1)因为an=f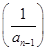 =
=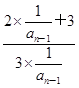 =an-1+
=an-1+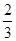 (n∈N*,且n≥2),
(n∈N*,且n≥2),
所以an-an-1=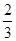 .因为a1=1,
.因为a1=1,
所以数列{an}是以1为首项,公差为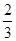 的等差数列.
的等差数列.
所以an=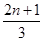 .
.
(2)①当n=2m,m∈N*时,
Tn=T2m=a1a2-a2a3+a3a4-a4a5+…+(-1)2m-1a2ma2m+1
=a2(a1-a3)+a4(a3-a5)+…+a2m(a2m-1-a2m+1)
=-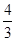 (a2+a4+…+a2m)=-
(a2+a4+…+a2m)=-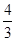 ×
×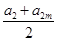 ×m
×m
=- (8m2+12m)=-
(8m2+12m)=- (2n2+6n).
(2n2+6n).
②当n=2m-1,m∈N*时,
Tn=T2m-1=T2m-(-1)2m-1a2ma2m+1=- (8m2+12m)+
(8m2+12m)+ (16m2+16m+3)
(16m2+16m+3)
= (8m2+4m+3)=
(8m2+4m+3)= (2n2+6n+7).
(2n2+6n+7).
所以Tn=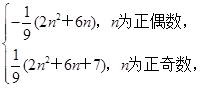 要使Tn≥tn2对n∈N*恒成立,只要使-
要使Tn≥tn2对n∈N*恒成立,只要使- (2n2+6n)≥tn2,(n为正偶数)恒成立.
(2n2+6n)≥tn2,(n为正偶数)恒成立.
只要使-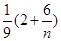 ≥t,对n∈N*恒成立,故实数t的取值范围为
≥t,对n∈N*恒成立,故实数t的取值范围为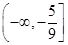
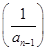 =
=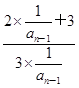 =an-1+
=an-1+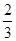 (n∈N*,且n≥2),
(n∈N*,且n≥2),所以an-an-1=
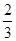 .因为a1=1,
.因为a1=1,所以数列{an}是以1为首项,公差为
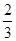 的等差数列.
的等差数列.所以an=
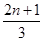 .
.(2)①当n=2m,m∈N*时,
Tn=T2m=a1a2-a2a3+a3a4-a4a5+…+(-1)2m-1a2ma2m+1
=a2(a1-a3)+a4(a3-a5)+…+a2m(a2m-1-a2m+1)
=-
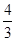 (a2+a4+…+a2m)=-
(a2+a4+…+a2m)=-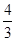 ×
×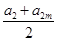 ×m
×m=-
 (8m2+12m)=-
(8m2+12m)=- (2n2+6n).
(2n2+6n).②当n=2m-1,m∈N*时,
Tn=T2m-1=T2m-(-1)2m-1a2ma2m+1=-
 (8m2+12m)+
(8m2+12m)+ (16m2+16m+3)
(16m2+16m+3)=
 (8m2+4m+3)=
(8m2+4m+3)= (2n2+6n+7).
(2n2+6n+7).所以Tn=
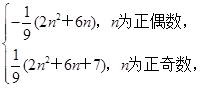 要使Tn≥tn2对n∈N*恒成立,只要使-
要使Tn≥tn2对n∈N*恒成立,只要使- (2n2+6n)≥tn2,(n为正偶数)恒成立.
(2n2+6n)≥tn2,(n为正偶数)恒成立.只要使-
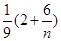 ≥t,对n∈N*恒成立,故实数t的取值范围为
≥t,对n∈N*恒成立,故实数t的取值范围为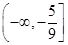

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
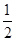 ,an+1=
,an+1=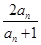 (n∈N*).
(n∈N*).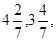 …的前n项和为Sn,则使得Sn取得最大值的n的值为( )
…的前n项和为Sn,则使得Sn取得最大值的n的值为( ) 中,
中, ,则
,则 的值为( )
的值为( )