题目内容
已知数列{an}满足:a1=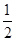 ,an+1=
,an+1=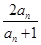 (n∈N*).
(n∈N*).
(1)求a2,a3的值;
(2)证明:不等式0<an<an+1对于任意n∈N*都成立.
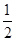 ,an+1=
,an+1=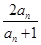 (n∈N*).
(n∈N*).(1)求a2,a3的值;
(2)证明:不等式0<an<an+1对于任意n∈N*都成立.
(1)a2=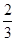 ,a3=
,a3=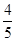 (2)见解析
(2)见解析
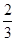 ,a3=
,a3=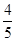 (2)见解析
(2)见解析(1)由题意,得a2=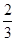 ,a3=
,a3=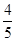 .
.
(2)①当n=1时,由(1)知0<a1<a2,不等式成立.
②设当n=k(k∈N*)时,0<ak<ak+1成立,则当n=k+1时,由归纳假设,知ak+1>0.
而ak+2-ak+1=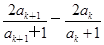 =
=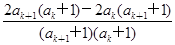 =
=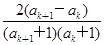 >0,
>0,
所以0<ak+1<ak+2,
即当n=k+1时,不等式成立.
由①②,得不等式0<an<an+1对于任意n∈N*成立.
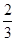 ,a3=
,a3=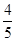 .
.(2)①当n=1时,由(1)知0<a1<a2,不等式成立.
②设当n=k(k∈N*)时,0<ak<ak+1成立,则当n=k+1时,由归纳假设,知ak+1>0.
而ak+2-ak+1=
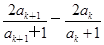 =
=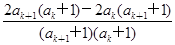 =
=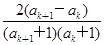 >0,
>0,所以0<ak+1<ak+2,
即当n=k+1时,不等式成立.
由①②,得不等式0<an<an+1对于任意n∈N*成立.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
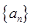 的前
的前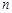 项和为
项和为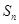 .
.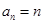 ,数列
,数列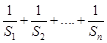 的和.
的和.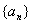 的首项
的首项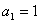 ,前
,前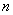 项和为
项和为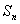 (
(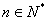 ),且点
),且点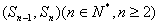 在直线
在直线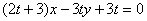 上(
上(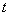 为与
为与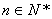 )为等比数列;
)为等比数列;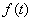 ,数列
,数列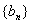 满足
满足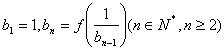 ,设
,设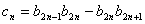 ,求数列
,求数列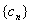 的前
的前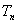 ;
;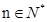 时不等式
时不等式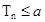 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。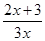 (x>0),数列{an}满足a1=1,an=f
(x>0),数列{an}满足a1=1,an=f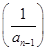 (n∈N*,且n≥2).
(n∈N*,且n≥2).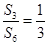 ,则
,则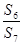 =________.
=________.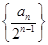 的前n项和.
的前n项和.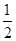
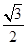
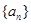 中,如果
中,如果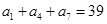 ,
,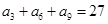 ,则数列
,则数列