题目内容
已知数列{an}是公差不为0的等差数列，{bn}是等比数列，其中a1＝3，b1＝1，a2＝b2,3a5＝b3，若存在常数u，v对任意正整数n都有an＝3logubn＋v，则u＋v＝________.
6
设等差数列{an}的公差为d，等比数列{bn}的公比为q，则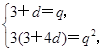
解得d＝6，q＝9，所以an＝6n－3，bn＝9n－1,6n－3＝3nlogu9＋v－3logu9对任意正整数n恒成立，所以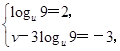
解得u＝v＝3，故u＋v＝6.
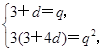解得d＝6，q＝9，所以an＝6n－3，bn＝9n－1,6n－3＝3nlogu9＋v－3logu9对任意正整数n恒成立，所以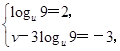 解得u＝v＝3，故u＋v＝6.
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
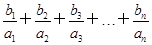<5.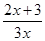
(x＞0)，数列{an}满足a1＝1，an＝f
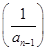(n∈N*，且n≥2)．
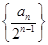的前n项和．
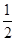a11＋6，则数列{an}前9项的和S9等于( )．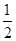
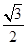
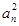＋anan＋1＝0，则它的通项公式为( )．
