题目内容
7．若（2x3+x-2）n的展开式中只有第6项的二项式系数最大，则展开式中的常数项是3360．分析 利用二项展开式的通项公式求出展开式的通项；利用二项式系数的性质：中间项的二项式系数最大求出n；将n的值代入通项；令通项中的x的指数为0求出r，将r的值代入通项求出展开式的常数项．
解答 解：∵展开式中，只有第6项的系数最大，
∴n=10，
∴展开式的通项为Tr+1=210-rC10rx30-5r，
令30-5r=0得r=6，
所以展开式中的常数项为24C106=3360．
故答案为：3360．
点评 本题考查利用二项展开式的通项解决二项展开式的特定项问题、考查二项式系数的性质：中间项的二项式系数最大．
练习册系列答案
相关题目
17．
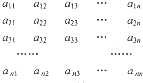如图所示，将n2（n≥9）个正数排成n行n列的数阵，其中的每一行都成等差数列，每一列都成等比数列，各等比数列的公比都相同且不为1，若a11=a22=a34=$\frac{1}{2}$，则a11+a22+a33+…+a99=（ ）
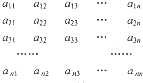如图所示，将n2（n≥9）个正数排成n行n列的数阵，其中的每一行都成等差数列，每一列都成等比数列，各等比数列的公比都相同且不为1，若a11=a22=a34=$\frac{1}{2}$，则a11+a22+a33+…+a99=（ ）| A． | $\frac{1031}{512}$ | B． | $\frac{1031}{512}$ | C． | $\frac{1013}{1024}$ | D． | $\frac{1031}{1024}$ |
7．
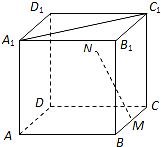如图，在正方体中ABCD-A1B1C1D1，M为BC的中点，点N在四边形CDD1C1及其内部运动．若MN⊥A1C1，则N点的轨迹为（ ）
如图，在正方体中ABCD-A1B1C1D1，M为BC的中点，点N在四边形CDD1C1及其内部运动．若MN⊥A1C1，则N点的轨迹为（ ）| A． | 线段 | B． | 圆的一部分 | C． | 椭圆的一部分 | D． | 双曲线的一部分 |