Question

【题目】数列{an}中，an=32，sn=63，
（1）若数列{an}为公差为11的等差数列，求a1；
（2）若数列{an}为以a1=1为首项的等比数列，求数列{am2}的前m项和sm′ ．

Answer 1

【答案】
（1）解：∵ ，

a1+（n﹣1）11=an=32

解得 a1=10

（2）解：

解得：q=2 n=6

∴所以{an2}是首项为1，公比为4的等比数列

∴Sm=

【解析】（1）由数列为等差数列，根据条件，用首项和公差分别表示通项和前n项和建立方程组求解．（2）由数列为等比数列，根据条件，用首项和公比分别表示通项和前n项和建立方程组求解．
【考点精析】通过灵活运用数列的前n项和，掌握数列{an}的前n项和sn与通项an的关系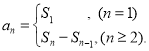即可以解答此题．