题目内容
【题目】如图所示，已知AB丄平面BCD，M、N分别是AC、AD的中点，BC 丄 CD.
（1）求证：MN//平面BCD；
（2）若AB=1，BC=
，求直线AC与平面BCD所成的角.
【答案】（1）见解析；（2）30°.
【解析】试题分析：（1）由中位线定理可得MN∥CD，进而得线面平行；
（2）由AB⊥平面BCD，知∠ACB为直线AC与平面BCD所成的角，在直角△ABC中求解即可.
试题解析：
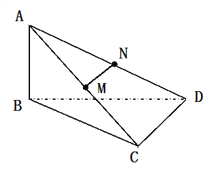
证明：（1）∵M，N分别是AC，AD的中点，
∴MN∥CD.∵MN平面BCD且CD平面BCD，
∴MN∥平面BCD.
（2）∵AB⊥平面BCD，∴∠ACB为直线AC与平面BCD所成的角.
在直角△ABC中,AB=1,BC=
，∴tan∠ACB=
.∴∠ACB=30°.
故直线AC与平面BCD所成的角为30°.
练习册系列答案
相关题目
