题目内容
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),以坐标原点为极点,
),以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)讨论直线![]() 与圆
与圆![]() 的公共点个数;
的公共点个数;
(Ⅱ)过极点作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,求点
,求点![]() 的轨迹与圆
的轨迹与圆![]() 相交所得弦长.
相交所得弦长.
【答案】(Ⅰ)见解析;(Ⅱ)点![]() 的轨迹与圆
的轨迹与圆![]() 相交所得弦长是
相交所得弦长是![]() .
.
【解析】试题分析: (Ⅰ)根据直线参数方程的几何意义可知直线![]() 式过定点
式过定点![]() ,将极坐标方程化为直角坐标,可知圆心为
,将极坐标方程化为直角坐标,可知圆心为![]() ,半径为
,半径为![]() ,动态讨论倾斜角可得结果;(Ⅱ)直线与圆的极坐标方程联立,求出极径,即可得结果.
,动态讨论倾斜角可得结果;(Ⅱ)直线与圆的极坐标方程联立,求出极径,即可得结果.
试题解析:(Ⅰ)直线![]() 式过定点
式过定点![]() ,倾斜角在
,倾斜角在![]() 内的一条直线,
内的一条直线,
圆![]() 的方程为
的方程为![]() ,∴当
,∴当![]() 时,直线
时,直线![]() 与圆
与圆![]() 有1个公共点;
有1个公共点;
当![]() 时,直线
时,直线![]() 与圆
与圆![]() 有2个公共点
有2个公共点
(Ⅱ)依题意,点![]() 在以
在以![]() 为直径的圆上,可得轨迹极坐标方程为
为直径的圆上,可得轨迹极坐标方程为![]() .
.
联立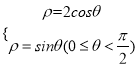 得
得![]() .
.
∴点![]() 的轨迹与圆
的轨迹与圆![]() 相交所得弦长是
相交所得弦长是![]() .
.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目