题目内容
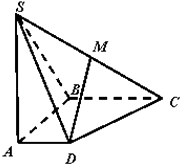
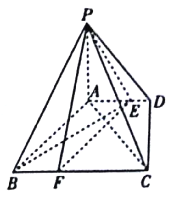
【题目】四棱锥![]() 中,
中, ![]() 面
面![]() ,底面
,底面![]() 是菱形,且
是菱形,且![]() ,
, ![]() ,过点
,过点![]() 作直线
作直线![]() ,
, ![]() 为直线
为直线![]() 上一动点.
上一动点.
(1)求证: ![]() ;
;
(2)当二面角![]() 的大小为
的大小为![]() 时,求
时,求![]() 的长;
的长;
(3)在(2)的条件下,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:
(1)利用三垂线定理结合![]() 即可证得
即可证得![]() ;
;
(2)首先写出二面角的平面角,最后利用余弦定理列出方程求解QB的长度即可;
(3)将问题转化为两个三棱锥的体积,其中公共的底为△POQ,高的总长度为AC的长,则体积公式为: ![]()
试题解析:
(1)由题意知直线![]() 在面
在面![]() 上的射影为
上的射影为![]() ,
,
又菱形![]() 中
中![]() ,由三垂线定理知
,由三垂线定理知![]() .
.
(2)![]() 和
和![]() 都是以
都是以![]() 为底的等腰三角形,设
为底的等腰三角形,设![]() 和
和![]() 的交点为
的交点为![]() ,
,

连接![]() ,则
,则![]() 是二面角
是二面角![]() 的平面角,
的平面角,
由![]() 知,二面角
知,二面角![]() 大于
大于![]() ,
,
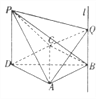
所以点![]() 与点
与点![]() 在平面
在平面![]() 的同侧,如图所示.
的同侧,如图所示.
则![]() 是二面角
是二面角![]() 的平面角,故
的平面角,故![]() .
.
在![]() 中,
中, ![]() ,设
,设![]() ,则
,则![]() 中,
中, ![]() ,
,
在直角梯形![]() 中,
中, ![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得![]() ,故
,故![]() 且
且![]() ,
,
解得![]() ,即
,即![]() .
.
(3)由(2)知: ![]() ,
, ![]() ,
,
且![]() 面
面![]() ,∴
,∴![]() .
.

练习册系列答案
相关题目