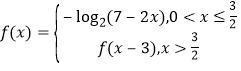题目内容
【题目】已知函数![]() .
.
(1)若![]() ,证明:当
,证明:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
(2)若![]() 是
是![]() 的极大值点,求
的极大值点,求![]() .
.
【答案】(1)见解析;(2)![]() .
.
【解析】分析:(1)对函数f(x)两次求导数,分别判断f′(x)和f(x)的单调性,结合f(0)=0即可得出结论;(2)令h(x)为f′(x)的分子,令h″(0)计算a,讨论a的范围,得出f(x)的单调性,从而得出a的值.
详解:
(1)证明:当a=0时,f(x)=(2+x)ln(1+x)﹣2x,(x>﹣1).
![]() ,
,![]() ,
,
可得x∈(﹣1,0)时,f″(x)≤0,x∈(0,+∞)时,f″(x)≥0
∴f′(x)在(﹣1,0)递减,在(0,+∞)递增,
∴f′(x)≥f′(0)=0,
∴f(x)=(2+x)ln(1+x)﹣2x在(﹣1,+∞)上单调递增,又f(0)=0.
∴当﹣1<x<0时,f(x)<0;当x>0时,f(x)>0.
(2)解:由f(x)=(2+x+ax2)ln(1+x)﹣2x,得
f′(x)=(1+2ax)ln(1+x)+![]() ﹣2=
﹣2=![]() ,
,
令h(x)=ax2﹣x+(1+2ax)(1+x)ln(x+1),
h′(x)=4ax+(4ax+2a+1)ln(x+1).
当a≥0,x>0时,h′(x)>0,h(x)单调递增,
∴h(x)>h(0)=0,即f′(x)>0,
∴f(x)在(0,+∞)上单调递增,故x=0不是f(x)的极大值点,不符合题意.
当a<0时,h″(x)=8a+4aln(x+1)+![]() ,
,
显然h″(x)单调递减,
①令h″(0)=0,解得a=﹣![]() .
.
∴当﹣1<x<0时,h″(x)>0,当x>0时,h″(x)<0,
∴h′(x)在(﹣1,0)上单调递增,在(0,+∞)上单调递减,
∴h′(x)≤h′(0)=0,
∴h(x)单调递减,又h(0)=0,
∴当﹣1<x<0时,h(x)>0,即f′(x)>0,
当x>0时,h(x)<0,即f′(x)<0,
∴f(x)在(﹣1,0)上单调递增,在(0,+∞)上单调递减,
∴x=0是f(x)的极大值点,符合题意;
②若﹣![]() <a<0,则h″(0)=1+6a>0,h″(e
<a<0,则h″(0)=1+6a>0,h″(e![]() ﹣1)=(2a﹣1)(1﹣e
﹣1)=(2a﹣1)(1﹣e![]() )<0,
)<0,
∴h″(x)=0在(0,+∞)上有唯一一个零点,设为x0,
∴当0<x<x0时,h″(x)>0,h′(x)单调递增,
∴h′(x)>h′(0)=0,即f′(x)>0,
∴f(x)在(0,x0)上单调递增,不符合题意;
③若a<﹣![]() ,则h″(0)=1+6a<0,h″(
,则h″(0)=1+6a<0,h″(![]() ﹣1)=(1﹣2a)e2>0,
﹣1)=(1﹣2a)e2>0,
∴h″(x)=0在(﹣1,0)上有唯一一个零点,设为x1,
∴当x1<x<0时,h″(x)<0,h′(x)单调递减,
∴h′(x)>h′(0)=0,∴h(x)单调递增,
∴h(x)<h(0)=0,即f′(x)<0,
∴f(x)在(x1,0)上单调递减,不符合题意.
综上,a=﹣![]() .
.