题目内容
【题目】已知定义域为![]() 的奇函数
的奇函数![]() ,当
,当![]() 时,满足
时,满足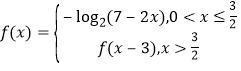 ,
,
则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】分析:通过计算前几项,可得n=3,4,…,2018,数列以3为周期的数列,计算可得所求和.
详解:定义域为R的奇函数f(x),可得f(﹣x)=﹣f(x),
当x>0时,满足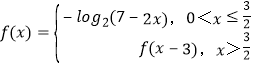 ,
,
可得x>![]() 时,f(x)=f(x﹣3),
时,f(x)=f(x﹣3),
则f(1)=﹣log25,
f(2)=f(﹣1)=﹣f(1)=log25,
f(3)=f(0)=0,
f(4)=f(1)=﹣log25,
f(5)=f(2)=f(﹣1)=﹣f(1)=log25,
f(6)=f(3)=f(0)=0,
f(7)=f(4)=f(1)=﹣log25,
f(8)=f(2)=f(﹣1)=﹣f(1)=log25,
…
f(1)+f(2)+f(3)+…+f(2020)
=﹣log25+log25+(0﹣log25+log25)×672 =0,
故选:D.

练习册系列答案
相关题目