Question

【题目】在直角坐标系xOy中，M（﹣2，0）．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，A（ρ，θ）为曲线C上一点，B（ρ，θ+ ），且|BM|=1．
（Ⅰ）求曲线C的直角坐标方程；
（Ⅱ）求|OA|2+|MA|2的取值范围．

Answer 1

【答案】解：（I）B（ρ，θ+ ），化为直角坐标：B ，
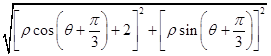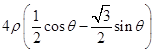∵|BM|=1，∴ =1，化为：ρ2+4ρ +3=0，展开：ρ2+ +3=0，
化为直角坐标方程：x2+y2+2x﹣2 y+3=0．
（II）：x2+y2+2x﹣2 y+3=0配方为：（x+1）2+ =1，可得圆心C ，半径r=1．
点P（﹣1，0）到圆心C的距离d= ．
A（ρ，θ）化为直角坐标A（x，y）．
∴|OA|2+|MA|2=x2+y2+（x+2）2+y2=2[（x+1）2+y2]+2∈[2×3﹣1+2，2×3+1+2]，即|OA|2+|MA|2∈[7，9]．
【解析】（I）B（ρ，θ+ ），化为直角坐标：B ，利用|BM|=1，可得ρ2+4ρ +3=0，展开把 及其ρ2=x2+y2代入即可得出．（II）x2+y2+2x﹣2 y+3=0配方为：（x+1）2+ =1，可得圆心C，半径r．得出点P（﹣1，0）到圆心C的距离d．A（ρ，θ）化为直角坐标A（x，y）．|OA|2+|MA|2=2[（x+1）2+y2]+2∈[2d2﹣1+2，2d2+1+2]．