Question

【题目】已知函数．

（1）当a=3时，方程的解的个数；

（2）对任意时，函数的图象恒在函数图象的下方，求a的取值范围；

（3）在上单调递增，求a的范围；

Answer 1

【答案】（1）当或时，方程有两个解；当或时，方程一个解；当时，方程有三个解；（2） （3）

【解析】

试题分析：（1）当a=3时，结合函数图像可得到m取不同范围时对应的方程的根的个数；（2）由题意得对任意的实数x∈[1，2]，f（x）＜g（x）恒成立，即x|x-a|＜1，当x∈[1，2]恒成立，由此能求出所有的实数a；（3）将函数式转化为分段函数,利用二次函数单调性求得其单调区间，与区间比较，从而得到a的不等式，求解其范围

试题解析：（1）当a=3时，，

当或时，方程有两个解；

当或时，方程一个解；

当时，方程有三个解.

（2） 由题意知恒成立，即在x∈[1,2]上恒成立，在x∈[1,2]上恒成立

在x∈[1,2]上恒成立，∴

（3）

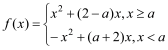
①且，即，f（x）在R单调递增，满足题意；

②且，即，f（x）在（∞，a）和（，+∞）单调递增，

∵f（x）在（-4，2）上单调递增，∴a≥2或-4，∴；

③且，即且，舍去；

④且，即，f（x）在（∞，）和（a，+∞）上单调递增，

∵f（x）在（-4，2）上单调递增，∴或a≤-4，∴a>2

综上：