Question

【题目】设f（x）=|x﹣3|+|x﹣4|．
（1）求函数 的定义域；
（2）若存在实数x满足f（x）≤ax﹣1，试求实数a的取值范围．

Answer 1

【答案】
（1）解：∵ ，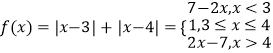

它与直线y=2交点的横坐标为 和 ．

∴不等式 的定义域为

（2）解：函数y=ax﹣1的图象是过点（0，﹣1）的直线，

作出图象，如下图：

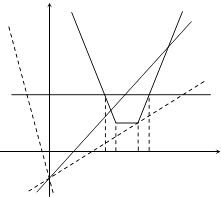
结合图象可知，a取值范围为

【解析】（1）求出f（x）=|x﹣3|+|x﹣4|与直线y=2交点的横坐标为 和 ，由此能求出不等式 的定义域．（2）函数y=ax﹣1的图象是过点（0，﹣1）的直线，作出图象，结合图象能求出实数a的取值范围．
【考点精析】掌握绝对值不等式的解法是解答本题的根本，需要知道含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号．