题目内容
【题目】成都七中为了解班级卫生教育系列活动的成效,对全校40个班级进行了一次突击班级卫生量化打分检查(满分100分,最低分20分).根据检查结果:得分在![]() 评定为“优”,奖励3面小红旗;得分在
评定为“优”,奖励3面小红旗;得分在![]() 评定为“良”,奖励2面小红旗;得分在
评定为“良”,奖励2面小红旗;得分在![]() 评定为“中”,奖励1面小红旗;得分在
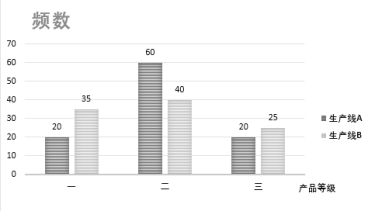
评定为“中”,奖励1面小红旗;得分在![]() 评定为“差”,不奖励小红旗.已知统计结果的部分频率分布直方图如下图:
评定为“差”,不奖励小红旗.已知统计结果的部分频率分布直方图如下图:
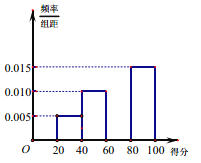
(1)依据统计结果的部分频率分布直方图,求班级卫生量化打分检查得分的中位数;
(2)学校用分层抽样的方法,从评定等级为“优”、“良”、“中”、“差”的班级中抽取10个班级,再从这10个班级中随机抽取2个班级进行抽样复核,记抽样复核的2个班级获得的奖励小红旗面数和为![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
【答案】(1)中位数为70分.(2)见解析,![]()
【解析】
(1)根据频率分布直方图中中位数的计算公式计算即可.
(2)先根据分层抽样确定10个班级中优”、“良”、“中”、“差”的班级的人数,再根据奖励小红旗的面数确定![]() 的可能取值,再根据古典概型概率计算公式求解
的可能取值,再根据古典概型概率计算公式求解![]() 每个取值对应的概率,最后列出分布列求解数学期望.
每个取值对应的概率,最后列出分布列求解数学期望.
解:(1)得分![]() 的频率为
的频率为![]() ;
;
得分![]() 的频率为
的频率为![]() ;
;
得分![]() 的频率为
的频率为![]() ;
;
所以得分![]() 的频率为
的频率为![]() .
.
设班级得分的中位数为![]() 分,于是
分,于是![]() ,解得
,解得![]() .
.
所以班级卫生量化打分检查得分的中位数为70分.
(2)由(1)知题意“优”、“良”、“中”、“差”的频率分别为0.3,0.4,0.2,0.1.又班级总数为40.于是“优”、“良”、“中”、“差”的班级个数分别为12,16,8,4.
分层抽样的方法抽取的“优”、“良”、“中”、“差”的班级个数分别为3,4,2,1.
由题意可得![]() 的所有可能取值为1,2,3,4,5,6.
的所有可能取值为1,2,3,4,5,6.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
所以![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
|
![]() .
.
所以![]() 的数学期望
的数学期望![]() .
.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案【题目】按照水果市场的需要等因素,水果种植户把某种成熟后的水果按其直径![]() 的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
d |
|
|
|
|
|
等级 | 三级品 | 二级品 | 一级品 | 特级品 | 特级品 |
频数 | 1 | m | 29 | n | 7 |
用分层抽样的方法从其中的一级品和特级品共抽取6个,其中一级品2个.
(1)估计这批水果中特级品的比例;
(2)已知样本中这批水果不按等级混装的话20个约1斤,该种植户有20000斤这种水果待售,商家提出两种收购方案:
方案A:以6.5元/斤收购;
方案B:以级别分装收购,每袋20个,特级品8元/袋,一级品5元/袋,二级品4元/袋,三级品3元/袋.
用样本的频率分布估计总体分布,问哪个方案种植户的收益更高?并说明理由.