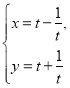题目内容
【题目】武汉市掀起了轰轰烈烈的“十日大会战”,要在10天之内,对武汉市民做一次全员检测,彻底摸清武汉市的详细情况.某医院为筛查冠状病毒,需要检验血液是否为阳性,现有![]() 份血液样本,有以下两种检验方式:
份血液样本,有以下两种检验方式:
方案①:将每个人的血分别化验,这时需要验1000次.
方案②:按![]() 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组![]() 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这![]() 个人的血就只需检验一次(这时认为每个人的血化验
个人的血就只需检验一次(这时认为每个人的血化验![]() 次);否则,若呈阳性,则需对这
次);否则,若呈阳性,则需对这![]() 个人的血样再分别进行一次化验这样,该组
个人的血样再分别进行一次化验这样,该组![]() 个人的血总共需要化验
个人的血总共需要化验![]() 次. 假设此次检验中每个人的血样化验呈阳性的概率为
次. 假设此次检验中每个人的血样化验呈阳性的概率为![]() ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.
(1)设方案②中,某组![]() 个人中每个人的血化验次数为
个人中每个人的血化验次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)设![]() . 试比较方案②中,
. 试比较方案②中,![]() 分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以减少多少次?(最后结果四舍五入保留整数)
分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以减少多少次?(最后结果四舍五入保留整数)
【答案】(1)分布列见解析;(2)![]() ,总次数为690次;
,总次数为690次;![]() ,总次数为604次;
,总次数为604次;![]() ,次数总为594次;减少406次
,次数总为594次;减少406次
【解析】
(1)设每个人的血呈阴性反应的概率为![]() ,可得
,可得![]() ,再由相互独立事件的概率求法可得
,再由相互独立事件的概率求法可得![]() 个人呈阴性反应的概率为
个人呈阴性反应的概率为![]() ,呈阳性反应的概率为
,呈阳性反应的概率为![]() ,随机变量
,随机变量![]() 即可得出分布列.
即可得出分布列.
(2)由(1)的分布列可求出数学期望,然后令![]() 求出期望即可求解.
求出期望即可求解.
(1)设每个人的血呈阴性反应的概率为![]() ,则
,则![]() .
.
所以![]() 个人的血混合后呈阴性反应的概率为
个人的血混合后呈阴性反应的概率为![]() ,呈阳性反应的概率为
,呈阳性反应的概率为![]() ,
,
依题意可知![]() ,
,
所以![]() 的分布列为:
的分布列为:

(2)方案②中,结合(1)知每个人的平均化验次数为:![]()
所以当![]() 时,
时, ![]() ,
,
此时1000人需要化验的总次数为690次,
![]()
![]() ,此时1000人需要化验的总次数为604次,
,此时1000人需要化验的总次数为604次,
![]() 时,
时, ![]() ,此时1000人需要化验的次数总为594次,
,此时1000人需要化验的次数总为594次,
即![]() 时化验次数最多,
时化验次数最多,![]() 时次数居中,
时次数居中,![]() 时化验次数最少.
时化验次数最少.
而采用方案①则需化验1000次,故在这三种分组情况下,相比方案①,
当![]() 时化验次数最多可以平均减少1000-594=406次.
时化验次数最多可以平均减少1000-594=406次.

【题目】新能源汽车已经走进我们的生活,逐渐为大家所青睐.现在有某品牌的新能源汽车在甲市进行预售,预售场面异常火爆,故该经销商采用竞价策略基本规则是:①竞价者都是网络报价,每个人并不知晓其他人的报价,也不知道参与竞价的总人数;②竞价采用“一月一期制”,当月竞价时间截止后,系统根据当期汽车配额,按照竞价人的出价从高到低分配名额.某人拟参加2020年6月份的汽车竞价,他为了预测最低成交价,根据网站的公告,统计了最近5个月参与竞价的人数(如下表)
月份 | 2020.01 | 2020.02 | 2020.03 | 2020.04 | 2020.05 |
月份编号 | 1 | 2 | 3 | 4 | 5 |
竞拍人数 | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)由收集数据的散点图发现,可用线性回归模型拟合竞价人数y(万人)与月份编号t之间的相关关系.请用最小二乘法求y关于t的线性回归方程:![]() ,并预测2020年6月份(月份编号为6)参与竞价的人数;
,并预测2020年6月份(月份编号为6)参与竞价的人数;
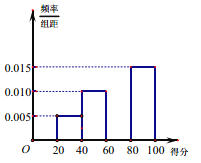
(2)某市场调研机构对200位拟参加2020年6月份汽车竞价人员的报价进行了一个抽样调查,得到如表所示的频数表:
报价区间(万元) |
|
|
|
|
|
|
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
(i)求这200位竞价人员报价的平均值![]() 和样本方差s2(同一区间的报价用该价格区间的中点值代替)
和样本方差s2(同一区间的报价用该价格区间的中点值代替)
(ii)假设所有参与竞价人员的报价X可视为服从正态分布![]() 且μ与σ2可分别由(i)中所示的样本平均数
且μ与σ2可分别由(i)中所示的样本平均数![]() 及s2估计.若2020年月6份计划提供的新能源车辆数为3174,根据市场调研,最低成交价高于样本平均数
及s2估计.若2020年月6份计划提供的新能源车辆数为3174,根据市场调研,最低成交价高于样本平均数![]() ,请你预测(需说明理由)最低成交价.
,请你预测(需说明理由)最低成交价.
参考公式及数据:
①回归方程![]() ,其中
,其中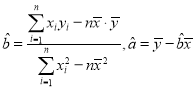
②![]()
③若随机变量X服从正态分布![]() 则
则![]()
![]() .
.
【题目】![]() 年
年![]() 月
月![]() 日,我国开始施行《个人所得税专项附加扣除操作办法》,附加扣除的专项包括子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人.某单位有老年员工
日,我国开始施行《个人所得税专项附加扣除操作办法》,附加扣除的专项包括子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人.某单位有老年员工![]() 人,中年员工
人,中年员工![]() 人,青年员工
人,青年员工![]() 人,现采用分层抽样的方法,从该单位员工中抽取
人,现采用分层抽样的方法,从该单位员工中抽取![]() 人,调查享受个人所得税专项附加扣除的情况,并按照员工类别进行各专项人数汇总,数据统计如表:
人,调查享受个人所得税专项附加扣除的情况,并按照员工类别进行各专项人数汇总,数据统计如表:
专项员工人数 | 子女教育 | 继续教育 | 大病医疗 | 住房贷款利息 | 住房租金 | 赡养老人 |
老员工 |
|
|
|
|
|
|
中年员工 |
|
|
|
|
|
|
青年员工 |
|
|
|
|
|
|
(Ⅰ)在抽取的![]() 人中,老年员工、中年员工、青年员工各有多少人;
人中,老年员工、中年员工、青年员工各有多少人;
(Ⅱ)从上表享受住房贷款利息专项扣除的员工中随机选取![]() 人,记
人,记![]() 为选出的中年员工的人数,求
为选出的中年员工的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.