题目内容
【题目】已知数列{an}的通项公式an＝﹣n2+8n﹣12，前n项和为Sn，若n＞m，则Sn﹣Sm的最大值是（ ）
A.5B.10C.15D.20
【答案】B
【解析】
由数列的通项公式可得Sn﹣Sm＝am+1+am+2+…+an，可得当am+1+am+2+…+an最大时，Sn﹣Sm取得最大值，由an≥0，解不等式，计算即可得到所求最大值．
解：根据题意，数列{an}的通项公式是
，
其前n项和是Sn，n＞m，有Sn﹣Sm＝am+1+am+2+…+an，
即当am+1+am+2+…+an最大时，Sn﹣Sm取得最大值；
若
，且n∈N+，解得2≤n≤6，
即当2≤n≤6时，an的值为正．
当n＝6，m＝2时，S6﹣S2＝a3+a4+a5+a6＝3+4+3+0＝10，
此时Sn﹣Sm取得最大值10．
故选：B．
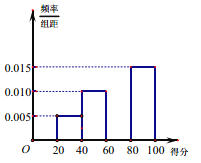
阅读快车系列答案
【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务，由于其依托“互联网+”，符合“低碳出行”的理念，已越来越多地引起了人们的关注.某部门为了对该市共享单车加强监管，随机选取了50人就该城市共享单车的推行情况进行问卷调查，并将问卷中的这50人根据其满意度评分值（百分制）按照
，
，……
分成5组，根据下面尚未完成并有局部污损的频率分布表和频率分布直方图（如图所示），计算
，
，
，
的值分别为（ ）
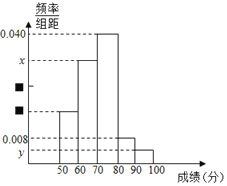
组别 | 分组 | 频数 | 频率 |
第1组 |
| 8 | 0.16 |
第2组 |
|
| ■ |
第3组 |
| 20 | 0.40 |
第4组 |
| ■ | 0.08 |
第5组 |
| 2 |
|
合计 | ■ | ■ |
A.16，0.04，0.032，0.004B.16，0.4，0.032，0.004
C.16，0.04，0.32，0.004D.12，0.04，0.032，0.04
【题目】为了调查某社区居民每天参加健身的时间，某机构在该社区随机采访男性、女性各50名，其中每人每天的健身时间不少于1小时称为“健身族”，否则称其为"非健身族”，调查结果如下：
健身族 | 非健身族 | 合计 | |
男性 | 40 | 10 | 50 |
女性 | 30 | 20 | 50 |
合计 | 70 | 30 | 100 |
（1）若居民每人每天的平均健身时间不低于70分钟，则称该社区为“健身社区”. 已知被随机采访的男性健身族，男性非健身族，女性健身族，女性非健身族每人每天的平均健分时间分別是1.2小时，0.8小时，1.5小时，0.7小时，试估计该社区可否称为“健身社区”？
（2）根据以上数据，能否在犯错误的概率不超过5%的情况下认为“健身族”与“性别”有关？
参考公式：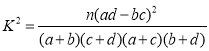 
，其中
.
参考数据：
| 0. 50 | 0. 40 | 0. 25 | 0. 05 | 0. 025 | 0. 010 |
| 0. 455 | 0. 708 | 1. 321 | 3. 840 | 5. 024 | 6. 635 |
