题目内容
【题目】已知抛物线![]() 的焦点为F,直线
的焦点为F,直线![]() 与x轴的交点为P,与抛物线的交点为Q,且
与x轴的交点为P,与抛物线的交点为Q,且![]() .
.

![]() 求抛物线的方程;
求抛物线的方程;
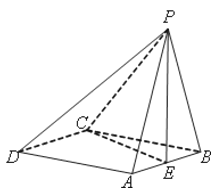
![]() 如图所示,过F的直线l与抛物线相交于
如图所示,过F的直线l与抛物线相交于![]() 两点,与圆
两点,与圆![]() 相交于
相交于![]() 两点
两点![]() 两点相邻
两点相邻![]() ,过
,过![]() 两点分别作抛物线的切线,两条切线相交于点M,求
两点分别作抛物线的切线,两条切线相交于点M,求![]() 与
与![]() 的面积之积的最小值.
的面积之积的最小值.
【答案】![]() 1
1![]() ;
;![]() 2
2![]() .
.
【解析】【试题分析】(I)根据抛物线的定义以及![]() ,解得
,解得![]() ,故抛物线的方程为
,故抛物线的方程为![]() .(II)设出直线
.(II)设出直线![]() 的方程,联立直线方程和抛物线方程,写出韦达定理,利用导数求得直线
的方程,联立直线方程和抛物线方程,写出韦达定理,利用导数求得直线![]() 的方程,联立两个方程求得点
的方程,联立两个方程求得点![]() 的坐标.利用点到直线距离公式求得
的坐标.利用点到直线距离公式求得![]() 到
到![]() 的距离,由此求得两个三角形面积乘积的表达式,进而求得最小值.
的距离,由此求得两个三角形面积乘积的表达式,进而求得最小值.
【试题解析】
![]() 由题意可知
由题意可知![]() ,丨QF丨
,丨QF丨![]() ,
,
由![]() ,则
,则![]() ,解得:
,解得:![]() ,
,
![]() 抛物线
抛物线![]() ;
;
![]() 设l:
设l:![]() ,
,
联立![]() ,整理得:
,整理得:![]() ,
,
则![]() ,
,
由![]() ,求导
,求导![]() ,
,
直线MA:![]() ,即
,即![]() ,
,
同理求得MD:![]() ,
,
 ,解得:
,解得:![]() ,则
,则![]() ,
,
![]() 到l的距离
到l的距离![]() ,
,
![]() 与
与![]() 的面积之积
的面积之积![]() 丨AB丨丨CD丨
丨AB丨丨CD丨![]() ,
,
![]() 丨AF丨
丨AF丨![]() 丨DF丨
丨DF丨![]() ,
,
![]() ,
,
![]() ,
,
当且仅当![]() 时取等号,
时取等号,
当![]() 时,
时,![]() 与
与![]() 的面积之积的最小值1.
的面积之积的最小值1.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如表所示:
商店名称 | A | B | C | D | E |
销售额(x)/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额(y)/百万元 | 2 | 3 | 3 | 4 | 5 |
(1)画出销售额和利润额的散点图.
(2)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程![]() =
=![]() x+
x+![]() ,其中
,其中![]() =
=![]() ,
,![]() =
=![]() -
-![]()
![]() .
.
(3)若获得利润是4.5百万元时估计销售额是多少(千万元)?