ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥ –ΡβΕ®2016Ρξ≥« –Ϋ®…ηAΘ§BΘ§C»ΐœν÷ΊΒψΙΛ≥ΧΘ§ΗΟ –“Μ¥σ–Ά≥«Ϋ®ΙΪΥΨΉΦ±Η≤ΈΦ”’β»ΐΗωΙΛ≥ΧΒΡΨΚ±ξΘ§ΦΌ…η’β»ΐΗωΙΛ≥ΧΨΚ±ξ≥…ΙΠ”κΖώœύΜΞΕάΝΔΘ§ΗΟΙΪΥΨΕ‘AΘ§BΘ§C»ΐœν÷ΊΒψΙΛ≥ΧΨΚ±ξ≥…ΙΠΒΡΗ≈¬ Ζ÷±πΈΣaΘ§bΘ§ ![]() Θ®aΘΨbΘ©Θ§“―÷Σ»ΐœνΙΛ≥ΧΕΦΨΚ±ξ≥…ΙΠΒΡΗ≈¬ ΈΣ
Θ®aΘΨbΘ©Θ§“―÷Σ»ΐœνΙΛ≥ΧΕΦΨΚ±ξ≥…ΙΠΒΡΗ≈¬ ΈΣ ![]() Θ§÷Ν…Ό”–“ΜœνΙΛ≥ΧΨΚ±ξ≥…ΙΠΒΡΗ≈¬ ΈΣ
Θ§÷Ν…Ό”–“ΜœνΙΛ≥ΧΨΚ±ξ≥…ΙΠΒΡΗ≈¬ ΈΣ ![]() Θ°
Θ°
Θ®1Θ©«σa”κbΒΡ÷ΒΘΜ
Θ®2Θ©ΙΪΥΨΉΦ±ΗΕ‘ΗΟΙΪΥΨ≤ΈΦ”AΘ§BΘ§C»ΐΗωœνΡΩΒΡΨΚ±ξΆ≈Ε”Ϋχ––Ϋ±άχΘ§AœνΡΩΨΚ±ξ≥…ΙΠΫ±άχ2Άρ‘ΣΘ§BœνΡΩΨΚ±ξ≥…ΙΠΫ±άχ4Άρ‘ΣΘ§CœνΡΩΨΚ±ξ≥…ΙΠΫ±άχ6Άρ‘ΣΘ§«σΨΚ±ξΆ≈Ε”ΜώΒΟΫ±άχΫπΕνΒΡΖ÷≤ΦΝ–”κ ΐ―ßΤΎΆϊΘ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚ”…Χβ“βΒΟ 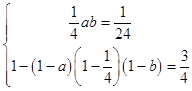 Θ§
Θ§
”…aΘΨbΘ§ΫβΒΟa= ![]() Θ§b=
Θ§b= ![]()
Θ®2Θ©ΫβΘΚ”…Χβ“βΘ§ΝνΨΚ±ξΆ≈Ε”ΜώΒΟΫ±άχΫπΕνΈΣΥφΜζ±δΝΩXΘ§‘ρXΒΡ÷ΒΩ…“‘ΈΣ0Θ§2Θ§4Θ§6Θ§8Θ§10Θ§
PΘ®X=0Θ©= ![]() Θ§
Θ§
PΘ®X=2Θ©= ![]() =
= ![]() Θ§
Θ§
PΘ®X=4Θ©= ![]() =
= ![]() Θ§
Θ§
PΘ®X=6Θ©= ![]() =
= ![]() Θ§
Θ§
PΘ®X=8Θ©= ![]() =
= ![]() Θ§
Θ§
PΘ®X=10Θ©= ![]() =
= ![]() Θ§
Θ§
PΘ®X=12Θ©= ![]() =
= ![]() Θ§
Θ§
ΓύXΒΡΖ÷≤ΦΝ–ΈΣΘΚ
X | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
P |
|
|
|
|
|
|
|
EΘ®XΘ©= ![]() +
+ ![]() =
= ![]() Θ°
Θ°
ΓΨΫβΈωΓΩΘ®1Θ©”…Χβ“βάϊ”ΟœύΜΞΕάΝΔ ¬ΦΰΗ≈¬ ≥ΥΖ®ΙΪ ΫΚΆΕ‘ΝΔ ¬ΦΰΗ≈¬ ΦΤΥψΙΪ ΫΝ–≥ωΖΫ≥ΧΉιΘ§Ρή«σ≥ωa”κbΒΡ÷ΒΘ°Θ®2Θ©”…Χβ“βΘ§ΝνΨΚ±ξΆ≈Ε”ΜώΒΟΫ±άχΫπΕνΈΣΥφΜζ±δΝΩXΘ§‘ρXΒΡ÷ΒΩ…“‘ΈΣ0Θ§2Θ§4Θ§6Θ§8Θ§10Θ§Ζ÷±π«σ≥ωœύ”ΠΒΡΗ≈¬ Θ§”…¥ΥΡή«σ≥ωXΒΡΖ÷≤ΦΝ–ΚΆEΘ®XΘ©Θ°
ΓΨΩΦΒψΨΪΈωΓΩΫβ¥π¥ΥΧβΒΡΙΊΦϋ‘Ύ”ΎάμΫβάκ…Δ–ΆΥφΜζ±δΝΩΦΑΤδΖ÷≤ΦΝ–ΒΡœύΙΊ÷Σ ΕΘ§’ΤΈ’‘Ύ…δΜςΓΔ≤ζΤΖΦλ―ιΒ»άΐΉ”÷–Θ§Ε‘”ΎΥφΜζ±δΝΩXΩ…Ρή»ΓΒΡ÷ΒΘ§Έ“Ο«Ω…“‘Α¥“ΜΕ®¥Έ–ρ“Μ“ΜΝ–≥ωΘ§’β―υΒΡΥφΜζ±δΝΩΫ–Ήωάκ…Δ–ΆΥφΜζ±δΝΩΘ°άκ…Δ–ΆΥφΜζ±δΝΩΒΡΖ÷≤ΦΝ–ΘΚ“ΜΑψΒΡ,…ηάκ…Δ–ΆΥφΜζ±δΝΩXΩ…Ρή»ΓΒΡ÷ΒΈΣx1,x2,.....,xi,......,xnΘ§X»ΓΟΩ“ΜΗω÷Β xi(i=1,2,......Θ©ΒΡΗ≈¬ P(ΠΈ=xiΘ©ΘΫPiΘ§‘ρ≥Τ±μΈΣάκ…Δ–ΆΥφΜζ±δΝΩX ΒΡΗ≈¬ Ζ÷≤ΦΘ§Φρ≥ΤΖ÷≤ΦΝ–Θ°

ΓΨΧβΡΩΓΩΙζΦ“…δΜςΕ”ΒΡΡ≥Ε”‘±…δΜς“Μ¥ΈΘ§Οϋ÷–7~10ΜΖΒΡΗ≈¬ »γ±μΥυ ΨΘΚ
Οϋ÷–ΜΖ ΐ | 10ΜΖ | 9ΜΖ | 8ΜΖ | 7ΜΖ |
Η≈¬ | 0.32 | 0.28 | 0.18 | 0.12 |
«σΗΟ…δΜςΕ”‘±…δΜς“Μ¥Έ «σ:
Θ®1Θ©…δ÷–9ΜΖΜρ10ΜΖΒΡΗ≈¬ ΘΜ
Θ®2Θ©÷Ν…ΌΟϋ÷–8ΜΖΒΡΗ≈¬ ΘΜΘ®3Θ©Οϋ÷–≤ΜΉψ8ΜΖΒΡΗ≈¬ ΓΘ


