题目内容
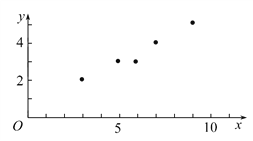
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如表所示:
商店名称 | A | B | C | D | E |
销售额(x)/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额(y)/百万元 | 2 | 3 | 3 | 4 | 5 |
(1)画出销售额和利润额的散点图.
(2)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程![]() =
=![]() x+
x+![]() ,其中
,其中![]() =
=![]() ,
,![]() =
=![]() -
-![]()
![]() .
.
(3)若获得利润是4.5百万元时估计销售额是多少(千万元)?
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)根据点坐标描点即可,(2)先求均值,代入公式求![]() 以及
以及![]() ,即得回归直线方程, (3)即求x=4.5时回归直线方程对应y值.
,即得回归直线方程, (3)即求x=4.5时回归直线方程对应y值.
试题解析:
(1)散点图如图所示:
(2)由已知数据计算得:
![]() =
=![]() =6,
=6,![]() =
=![]() =3.4,
=3.4,
![]() =200,
=200,![]() xiyi=112,
xiyi=112,
所以![]() =
=![]() =0.5,
=0.5,
则![]() =
=![]() -
-![]()
![]() =3.4-0.5×6=0.4,所以利润额y对销售额x的回归直线方程为
=3.4-0.5×6=0.4,所以利润额y对销售额x的回归直线方程为![]() =0.5x+0.4.
=0.5x+0.4.
(3)当y=4.5时,4.5=0.5x+0.4,计算得出x=8.2,
所以若获得利润是4.5百万元时估计销售额是8.2千万元.

练习册系列答案
相关题目
【题目】国家射击队的某队员射击一次,命中7~10环的概率如表所示:
命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求该射击队员射击一次 求:
(1)射中9环或10环的概率;
(2)至少命中8环的概率;(3)命中不足8环的概率。



