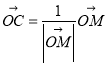题目内容
【题目】已知函数![]() 满足如下条件:
满足如下条件:
①函数![]() 的最小值为
的最小值为![]() ,最大值为9;
,最大值为9;
②![]() 且
且![]() ;
;
③若函数![]() 在区间
在区间![]() 上是单调函数,则
上是单调函数,则![]() 的最大值为2.
的最大值为2.
试探究并解决如下问题:
(Ⅰ)求![]() ,并求
,并求![]() 的值;
的值;
(Ⅱ)求函数![]() 的图象的对称轴方程;
的图象的对称轴方程;
(Ⅲ)设![]() 是函数
是函数![]() 的零点,求
的零点,求![]() 的值的集合.
的值的集合.
【答案】(Ⅰ)![]() ;
;![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)由函数![]() 的最值结合三角函数的最值可求得
的最值结合三角函数的最值可求得![]() ,
,![]() ;由函数
;由函数![]() 在区间
在区间![]() 上是单调函数,则
上是单调函数,则![]() 的最大值为2,可得
的最大值为2,可得![]() ,根据
,根据![]() 即可得
即可得![]() ;由
;由![]() 且
且![]() ,可得
,可得![]() ,验证即可得
,验证即可得![]() ;再由函数周期性即可得
;再由函数周期性即可得![]() ;
;
(Ⅱ)由题意结合三角函数的性质可令![]() ,化简即可得解;
,化简即可得解;
(Ⅲ)由题意可得![]() ,进而可得
,进而可得![]() ,
,
或![]() ,或
,或![]() ,化简后代入
,化简后代入![]() ,分别求解即可.
,分别求解即可.
(Ⅰ)因为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
所以![]() .
.
设![]() 的最小正周期为
的最小正周期为![]() ,
,
因为![]() 在区间
在区间![]() 上是单调函数,则
上是单调函数,则![]() 的最大值为2,
的最大值为2,
所以![]() ,所以
,所以![]() ,所以
,所以![]() 即
即![]() ,
,
所以![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() .
.
因为![]() ,所以
,所以![]() 或
或![]() .
.
若![]() ,则
,则![]() ,此时
,此时![]() ,不合题意;
,不合题意;
若![]() ,则
,则![]() ,此时
,此时![]() ,符合题意;
,符合题意;
所以![]() .
.
所以![]() .
.
因为![]() 的最小正周期为4,
的最小正周期为4,
所以![]() .
.
(Ⅱ)由(Ⅰ)知![]() .
.
令![]() ,得
,得![]() .
.
所以函数![]() 的对称轴方程是
的对称轴方程是![]() .
.
(Ⅲ)令![]() ,则
,则![]() ,所以函数
,所以函数![]() 的零点都满足:
的零点都满足:
![]() 或
或![]() .
.
因为![]() ,
,![]() 是函数
是函数![]() 的零点,所以
的零点,所以![]() ,
,
或![]() ,或
,或![]() ,
,
即![]() ,或
,或![]() ,
,
或![]() .
.
所以![]() ,
,
或![]() ,
,
或![]() .
.
故![]() 的值的集合为
的值的集合为![]() .
.

练习册系列答案
相关题目
【题目】恩格尔系数(记为![]() )是指居民的食物支出占家庭消费总支出的比重.国际上常用恩格尔系数来衡量一个国家和地区人民生活水平的状况.联合国对消费水平的规定标准如下表:
)是指居民的食物支出占家庭消费总支出的比重.国际上常用恩格尔系数来衡量一个国家和地区人民生活水平的状况.联合国对消费水平的规定标准如下表:
家庭类型 | 贫穷 | 温饱 | 小康 | 富裕 | 最富裕 |
|
|
|
|
|
|
实施精准扶贫以来,根据对某山区贫困家庭消费支出情况(单位:万元)的抽样调查,2018年每个家庭平均消费支出总额为2万元,其中食物消费支出为1.2万元预测2018年到2020年每个家庭平均消费支出总额每年的增长率约是30%,而食物消费支出平均每年增加0.2万元,预测该山区的家庭2020年将处于( )
A.贫困水平B.温饱水平C.小康水平D.富裕水平