Question

【题目】如图，四边形ABCD是梯形，AD∥BC，∠BAD=90°，四边形CC1D1D为矩形，已知AB⊥BC1，AD=4，AB=2，BC=1.

（I）求证：BC1∥平面ADD1；

（II）若DD1=2，求平面AC1D1与平面ADD1所成的锐二面角的余弦值；

（III）设P为线段C1D上的一个动点（端点除外），判断直线BC1与直线CP能否垂直?并说明理由.

Answer 1

【答案】（I）证明见解析；（II）；（III）直线BC1与CP不可能垂直.

【解析】试题分析：（1）先根据线面平行的判定定理证明平面平面，再由面面垂直的判定定理可得平面平面，根据面面平行的性质可得结果；（2）先证明平面，过在底面中作，所以, 两两垂直，以分别为轴、轴和轴，建立空间直角坐标系，求出平面与平面的法向量，利用空间向量夹角余弦公式可得结果；（3）利用反证法，若两直线垂直，根据向量垂直数量积为零可得到点不在线段上，从而假设不成立.

试题解析：（I）证明：由CC1D1D为矩形，得CC1∥DD1，又因为DD1平面ADD1，CC1平面ADD1，

所以CC1∥平面ADD1，

同理BC∥平面ADD1，又因为BCCC1=C，所以平面BCC1∥平面ADD1，

又因为BC1平面BCC1，所以BC1∥平面ADD1.

（II）.由平面ABCD中，AD∥BC，∠BAD=90°，得AB⊥BC，又因为AB⊥BC1，BCBC1=B，所以AB⊥平面BCC1，所以AB⊥CC1，又因为四边形CC1D1D为矩形，且底面ABCD中AB与CD相交一点，所以CC1⊥平面ABCD，因为CC1∥DD1，所以DD1⊥平面ABCD.

过D在底面ABCD中作DM⊥AD，所以DA，DM，DD1两两垂直，以DA，DM，DD1分别为x轴、y轴和z轴，如图建立空间直角坐标系，

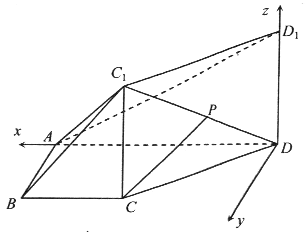
则D（0，0，0），A（4，0，0），B（4，2，0），C（3，2，0），C1（3，2，2），D1（0，0，2），

所以=（-l，2，2），=（-4，0，2）.

设平面AC1D1的一个法向量为m=（x，y，z），

由m·=0，m·=0，得

令x=2，得m=（2，-3，4）

易得平面ADD1的法向量n=（0，1，0）.

所以cos<m，n>=.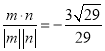

即平面AC1D1与平面ADD1所成的锐二面角的余弦值为

（III）结论：直线BC1与CP 不可能垂直，

证明：设DD1=m（m>0），= （∈（0，1）），

由B（4，2，0），C（3，2，0），C1（3，2，m），D（0，0，0），

得=（-l，0，m），=（3，2，m），= =（3，2，m），=（-3，-2，0），=+=（3-3，2-2，m）.

若BC1⊥CP，则·=-（3-3）+m2=0，即（m2-3）=-3，因为≠0，

所以m2=-+3>0，解得>1，这与0<<l矛盾.

所以直线BC1与CP不可能垂直.

【方法点晴】本题主要考查线面平行的判定定理利用空间向量求二面角，属于难题.空间向量解答立体几何问题的一般步骤是：（1）观察图形，建立恰当的空间直角坐标系；（2）写出相应点的标，求出相应直线的方向向量；（3）设出相应平面的法向量，利用两直线垂直数量积为零列出方程组求出法向量；（4）将空间位置关系转化为向量关系；（5）根据定理结论求出相应的角和距离.