题目内容
【题目】如图,在三棱锥![]() 中,
中, ![]() 底面
底面![]() ,
,![]() .
. ![]() 、
、![]() 分别为
分别为![]() 和
和![]() 的中点.
的中点. ![]() 为侧棱
为侧棱![]() 上的动点.
上的动点.
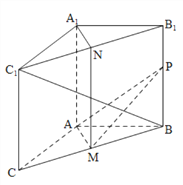
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)试判断直线![]() 与平面
与平面![]() 是否能够垂直.若能垂直,求
是否能够垂直.若能垂直,求![]() 的值;若不能垂直,请说明理由.
的值;若不能垂直,请说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ) ![]() .
.
【解析】试题分析:
(Ⅰ)由题意结合几何关系可证得![]() 是平行四边形,则
是平行四边形,则![]() ,
, ![]() 平面
平面![]()
(Ⅱ)由题意结合几何关系可证得![]() ,
, ![]() ,则
,则![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ;
;
(Ⅲ)原命题成立,则仅需在平面![]() 内再找一条和
内再找一条和![]() 相交的直线和
相交的直线和![]() 即可.考查
即可.考查![]() 的情况,结合相似三角形的性质可得
的情况,结合相似三角形的性质可得![]() .
.
试题解析:
(Ⅰ)证明:∵![]() 是三棱柱,
是三棱柱,
∴三个侧面都是平行四边形, ![]() 且
且![]() ,
,
又∵![]() 、
、![]() 分别为
分别为![]() 和
和![]() 的中点,
的中点,
∴![]() 且
且![]() ,
,
∴![]() 且
且![]() ,
,
∴![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)证明:∵![]() 底面
底面![]() ,
,
∴![]() 底面
底面![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
又∵![]() 是
是![]() 中点,
中点,
∴![]() ,
,
∵![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
则平面![]() 平面
平面![]() ;
;
(Ⅲ)直线![]() 与平面
与平面![]() 能够垂直,且
能够垂直,且![]() ,
,
由(Ⅱ)知![]() 平面
平面![]() ,
,
∴![]() ,
,
若要使![]() 平面
平面![]() ,仅需在平面
,仅需在平面![]() 内再找一条和
内再找一条和![]() 相交的直线和
相交的直线和![]() 即可.
即可.
此时我们取平面![]() 内和
内和![]() 相交的直线
相交的直线![]() ,
,
若![]() ,则
,则![]() 与
与![]() 相似,
相似,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目