题目内容
【题目】在推导很多三角恒等变换公式时,我们可以利用平面向量的有关知识来研究,在一定程度上可以简化推理过程.如我们就可以利用平面向量来推导两角差的余弦公式:![]()
具体过程如下:
如图,在平面直角坐标系![]() 内作单位圆O,以
内作单位圆O,以![]() 为始边作角
为始边作角![]() .它们的终边与单位圆O的交点分别为A,B.
.它们的终边与单位圆O的交点分别为A,B.

则![]()
由向量数量积的坐标表示,有:
![]()
设![]() 的夹角为θ,则
的夹角为θ,则
![]()
另一方面,由图3.1—3(1)可知,![]() ;由图可知,
;由图可知,

![]() .于是
.于是![]() .
.
所以![]() ,也有
,也有![]() ,
,
所以,对于任意角![]() 有:
有:![]() (
(![]() )
)
此公式给出了任意角![]() 的正弦、余弦值与其差角
的正弦、余弦值与其差角![]() 的余弦值之间的关系,称为差角的余弦公式,简记作
的余弦值之间的关系,称为差角的余弦公式,简记作![]() .
.
有了公式![]() 以后,我们只要知道
以后,我们只要知道![]() 的值,就可以求得
的值,就可以求得![]() 的值了.
的值了.
阅读以上材料,利用下图单位圆及相关数据(图中M是AB的中点),采取类似方法(用其他方法解答正确同等给分)解决下列问题:
(1)判断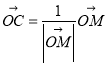 是否正确?(不需要证明)
是否正确?(不需要证明)
(2)证明:![]()
(3)利用以上结论求函数![]() 的单调区间.
的单调区间.
【答案】(1)正确;(2)见解析;(3)单调递增区间为![]() ,
,
![]() 的单调递减区间为
的单调递减区间为![]()
【解析】
(1) 因为对![]() 是
是![]() 方向上的单位向量,又
方向上的单位向量,又![]() 且
且![]() 与
与![]() 共线,即可判断出正确;
共线,即可判断出正确;
(2)在![]() 中,
中, ![]() ,又
,又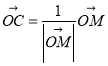 ,表示出
,表示出![]() ,
,![]() 的坐标,由纵坐标对应相等化简即可证得结论;
的坐标,由纵坐标对应相等化简即可证得结论;
即![]()
(3)由(2)结论化简可得 借助正弦型函数的性质即可求得结果.
借助正弦型函数的性质即可求得结果.
(1) 因为对于非零向量 是
是![]() 方向上的单位向量,又
方向上的单位向量,又![]() 且
且![]() 与
与![]() 共线,所以
共线,所以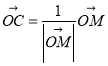 正确;
正确;
(2) 因为M为AB的中点,则![]() ,从而在
,从而在![]() 中,
中, ![]() ,又
,又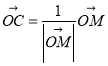 ,又
,又![]() ,
,![]() ,所以
,所以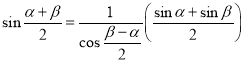 ,
,
即![]()
(3) 因为 令
令![]() ,解得:
,解得: ![]()
所以![]() 的单调递增区间为
的单调递增区间为![]()
令![]() ,解得:
,解得: ![]()
所以![]() 的单调递减区间为
的单调递减区间为![]()

练习册系列答案
相关题目


