题目内容
顶点在原点，焦点在x轴上，且截直线2x-y+1=0所得弦长为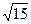
，求抛物线方程.
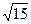，求抛物线方程.y2=12x或y2=-4x.
设所求抛物线方程为y2="ax(a≠0), " ①
直线方程变形为y="2x+1. " ②
设抛物线截直线所得弦长为|AB|，且A(x1,y1),B(x2,y2).
②代入①并整理得4x2+(4-a)x+1=0.
由韦达定理得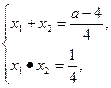
∴|AB|=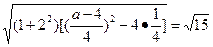
.
解得a=12或a=-4.∴所求抛物线方程为y2=12x或y2=-4x.
直线方程变形为y="2x+1. " ②
设抛物线截直线所得弦长为|AB|，且A(x1,y1),B(x2,y2).
②代入①并整理得4x2+(4-a)x+1=0.
由韦达定理得
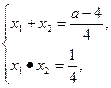
∴|AB|=
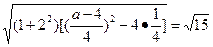.解得a=12或a=-4.∴所求抛物线方程为y2=12x或y2=-4x.
练习册系列答案
相关题目
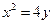上一点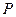
到焦点的距离为2,则点
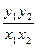的值为________________.
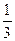x2上的两点A与B的横坐标恰好是关于x的方程x2+px+q=0(p、q∈R,p、q是常数)的两个实根,则直线AB的方程是_____________.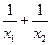
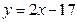上，另外两个顶点在抛物线
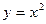上.则该正方形面积的最小值为 .