题目内容
抛物线y=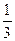 x2上的两点A与B的横坐标恰好是关于x的方程x2+px+q=0(p、q∈R,p、q是常数)的两个实根,则直线AB的方程是_____________.
x2上的两点A与B的横坐标恰好是关于x的方程x2+px+q=0(p、q∈R,p、q是常数)的两个实根,则直线AB的方程是_____________.
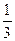 x2上的两点A与B的横坐标恰好是关于x的方程x2+px+q=0(p、q∈R,p、q是常数)的两个实根,则直线AB的方程是_____________.
x2上的两点A与B的横坐标恰好是关于x的方程x2+px+q=0(p、q∈R,p、q是常数)的两个实根,则直线AB的方程是_____________.px+3y+q=0(p2-4q>0)
设A(x1,y1),B(x2,y2),AB的中点M(x0,y0),
则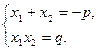
由点差法得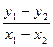 =
=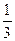 (x1+x2)=-
(x1+x2)=-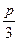 ,
,
即kAB=-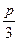 .
.
又x0=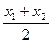 =-
=-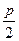 ,
,
y0=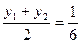 (x12+x22)=
(x12+x22)=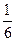 [(x1+x2)2-2x1x2]=
[(x1+x2)2-2x1x2]=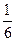 (p2-2q),
(p2-2q),
∴M(-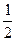 p,
p,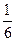 (p2-2q)).
(p2-2q)).
∴AB的方程为y-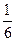 (p2-2q)=-
(p2-2q)=-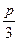 (x+
(x+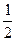 p),即px+3y+q=0(p2-4q>0).
p),即px+3y+q=0(p2-4q>0).
则
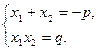
由点差法得
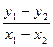 =
=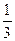 (x1+x2)=-
(x1+x2)=-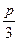 ,
,即kAB=-
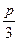 .
.又x0=
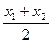 =-
=-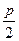 ,
,y0=
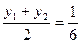 (x12+x22)=
(x12+x22)=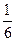 [(x1+x2)2-2x1x2]=
[(x1+x2)2-2x1x2]=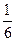 (p2-2q),
(p2-2q),∴M(-
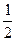 p,
p,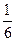 (p2-2q)).
(p2-2q)).∴AB的方程为y-
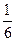 (p2-2q)=-
(p2-2q)=-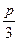 (x+
(x+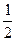 p),即px+3y+q=0(p2-4q>0).
p),即px+3y+q=0(p2-4q>0).
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
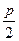 的点到其焦点F的距离;
的点到其焦点F的距离;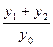 的值,并证明直线AB的斜率是非零常数.
的值,并证明直线AB的斜率是非零常数.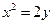 的准线方程是( )
的准线方程是( )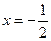
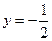
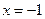
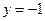
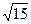 ,求抛物线方程.
,求抛物线方程.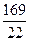 x
x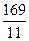 x
x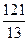 y
y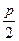 ),则点M的横坐标是( )
),则点M的横坐标是( )