题目内容
17.(1)化简:\frac{{cos(α+\frac{π}{2})}}{{sin(\frac{5π}{2}+α)}}•cos(α-π)+\frac{sin(-α)}{tan(α+π)};(2)已知tanα=2,求\frac{sinα+2cosα}{2sinα-cosα}的值.
分析 (1)原式利用诱导公式化简,整理即可得到结果;
(2)原式分子分母除以cosα,利用同角三角函数间的基本关系化简,把tanα的值代入计算即可求出值.
解答 解:(1)原式=\frac{-sinα}{cosα}•(-cosα)+\frac{-sinα}{\frac{sinα}{cosα}}=sinα-cosα;
(2)∵tanα=2,∴原式=\frac{tanα+2}{2tanα-1}=\frac{4}{3}.
点评 此题考查了同角三角函数间基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
8.当n为正整数时,定义函数N(n)表示n的最大奇因数.如N(3)=3,N(10)=5,….记S(n)=N(1)+N(2)+N(3)+…+N(2n),则S(4)等于( )
| A. | 81 | B. | 82 | C. | 85 | D. | 86 |
8.已知f(x)=sinx+cosx,且f1(x)=f′(x),fn+1(x)=fn′(x)(n∈N*),则f2015(x)=( )
| A. | -sinx-cosx | B. | cosx-sinx | C. | sinx-cosx | D. | sinx+cosx |
5.已知某四棱锥的三视图(单位:cm)如图所示,则该四棱锥的体积是( )


| A. | \frac{{\sqrt{3}}}{3}c{m^3} | B. | \frac{{4\sqrt{3}}}{3}c{m^3} | C. | \frac{{8\sqrt{3}}}{3}c{m^3} | D. | \sqrt{3}c{m^3} |
12.直线l过点(2,3)且与直线m:3x+2y-4=0垂直,则直线l的方程为( )
| A. | 3x+2y-12=0 | B. | 2x+3y-13=0 | C. | 3x-2y=0 | D. | 2x-3y+5=0 |
9.用火柴棒摆“金鱼”,如图所示:
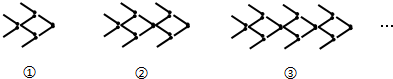
按照上面的规律,第10个“金鱼”图需要火柴棒的根数为( )

按照上面的规律,第10个“金鱼”图需要火柴棒的根数为( )
| A. | 58 | B. | 78 | C. | 62 | D. | 82 |
6.已知等轴双曲线经过点M(5,-4),则它的标准方程为( )
| A. | \frac{x^2}{9}-\frac{y^2}{9}=1 | B. | \frac{{y}^{2}}{9}-\frac{{x}^{2}}{9}=1 | ||
| C. | \frac{x^2}{9}-\frac{y^2}{9}=1或\frac{{y}^{2}}{9}-\frac{{x}^{2}}{9}=1 | D. | \frac{{x}^{2}}{41}-\frac{{y}^{2}}{41}=1 |
7.若角α的终边与单位圆相交于点(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}),则sinα的值为( )
| A. | \frac{\sqrt{2}}{2} | B. | -\frac{\sqrt{2}}{2} | C. | \frac{1}{2} | D. | -1 |