题目内容
若函数f(x)=x3-mx2+mx+3m在(0,1)内有极大值,无极小值,则( )
| A、m<0 | B、m<3 |
| C、m>3 | D、0<m<3 |
考点:利用导数研究函数的极值
专题:计算题,导数的综合应用
分析:由题意f′(x)=3x2-2mx+m在(0,1)上先正后负;结合二次函数可得f′(0)=m>0,f′(1)=3-2m+m<0;从而解得.
解答:
解:∵f(x)=x3-mx2+mx+3m,
∴f′(x)=3x2-2mx+m,
又∵f(x)=x3-mx2+mx+3m在(0,1)内有极大值,无极小值;
∴f′(x)=3x2-2mx+m在(0,1)上先正后负;
∴则f′(0)=m>0,f′(1)=3-2m+m<0;
故m>3;
故选C.
∴f′(x)=3x2-2mx+m,
又∵f(x)=x3-mx2+mx+3m在(0,1)内有极大值,无极小值;
∴f′(x)=3x2-2mx+m在(0,1)上先正后负;
∴则f′(0)=m>0,f′(1)=3-2m+m<0;
故m>3;
故选C.
点评:本题考查了导数的应用及二次函数的性质,属于中档题.

练习册系列答案
相关题目
已知F1(-c,0),F2(c,0)是双曲线C:
-
=1(a>0,b>0)的左右焦点,若p为双曲线右支上一点,满足
•
=4ac,∠F1PF2=
,则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| π |
| 3 |
A、2
| ||||
B、
| ||||
| C、2 | ||||
D、
|
已知集合A={y|y=x2-2},集合B={x|y=x2-1},则有( )
| A、A=B | B、A∩B=φ |
| C、A∪B=A | D、A∩B=A |
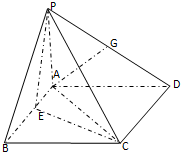 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G点,E点在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G点,E点在AB上,平面PEC⊥平面PDC.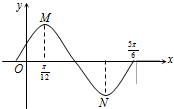 如图是函数y=Asin(ωx+φ)(A>0,ω>0|φ|<
如图是函数y=Asin(ωx+φ)(A>0,ω>0|φ|<