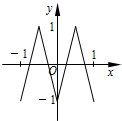题目内容
12.已知曲线C的极坐标方程为ρ2=$\frac{6}{2co{s}^{2}θ+3si{n}^{2}θ}$,以极点为平面直角坐标系的原点,极轴为x轴的正半轴建立平面直角坐标系.(Ⅰ)求曲线C的普通方程;
(Ⅱ)P,Q是曲线C上的两个点,当OP⊥OQ时,求$\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$的值.
分析 (I)曲线C的极坐标方程为ρ2=$\frac{6}{2co{s}^{2}θ+3si{n}^{2}θ}$,化为2ρ2cos2θ+3ρ2sin2θ=6,把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入即可得出.
(II)当直线OP,OQ的斜率都存在且不为0时,设直线OP:y=kx,则OQ的方程为:y=-$\frac{1}{k}$x.分别与椭圆方程联立解出即可得出.
解答 解:(I)曲线C的极坐标方程为ρ2=$\frac{6}{2co{s}^{2}θ+3si{n}^{2}θ}$,化为2ρ2cos2θ+3ρ2sin2θ=6,∴2x2+3y2=6,即$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$.
(II)当直线OP,OQ的斜率都存在且不为0时,
设直线OP:y=kx,∵OP⊥OQ,则OQ的方程为y=-$\frac{1}{k}$x.
联立$\left\{\begin{array}{l}{y=kx}\\{\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,解答x2=$\frac{6}{2+3{k}^{2}}$,y2=$\frac{6{k}^{2}}{2+3{k}^{2}}$,∴|OP|2=x2+y2=$\frac{6+6{k}^{2}}{2+3{k}^{2}}$,
把k换成$-\frac{1}{k}$可得:|OQ|2=$\frac{6+6{k}^{2}}{2{k}^{2}+3}$,
∴$\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$=$\frac{2+3{k}^{2}}{6+6{k}^{2}}$+$\frac{2{k}^{2}+3}{6+6{k}^{2}}$=$\frac{5}{6}$.
当直线OP,OQ的斜率一个为0而另一个不存在时,也成立.
综上可得:$\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$=$\frac{5}{6}$.
点评 本题考查了极坐标方程化为直角坐标方程、直线与椭圆相交问题、两点之间的距离公式、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于中档题.

| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
| A. | ∅ | B. | {0} | C. | {0,1} | D. | {2,0,1,5} |
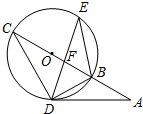 如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的
如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的下列结论中,错误的是( )
| A. | AB=2 | B. | $\frac{BF}{DF}$=$\frac{EF}{CF}$ | C. | ∠E=30° | D. | △EBD∽△CDB |
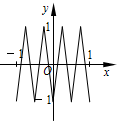
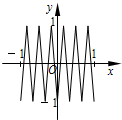
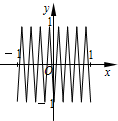
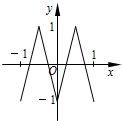 如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )