题目内容
14.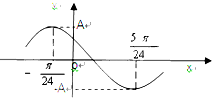 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )| A. | -$\sqrt{3}$ | B. | -1-$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | -1+$\sqrt{3}$ |
分析 由图象和已知条件易得函数的解析式,由周期性和可化简要求的式子,代值计算可得.
解答 解:由图象易得函数的周期T满足$\frac{T}{2}$=$\frac{π}{ω}$=$\frac{5π}{24}$-(-$\frac{π}{24}$),
解得ω=4,∴函数的周期T=$\frac{π}{2}$,
又封闭图形的面积π=$\frac{1}{2}$×$\frac{π}{2}$×2A,∴A=2,
∴f(x)=2sin(4x+φ),
代点(-$\frac{π}{24}$,2)可得2sin(-$\frac{π}{6}$+φ)=2,
结合0<φ<π可得φ=$\frac{2π}{3}$,
∴f(x)=2sin(4x+$\frac{2π}{3}$),
由图象可得一个周期内的函数值之和比如f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+f($\frac{4π}{8}$)=0,
∴f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8}$)
=f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)=0-f($\frac{4π}{8}$)=-$\sqrt{3}$
故选:A
点评 本题考查三角函数图象求解析式,涉及三角函数的周期性,属中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
4.已知双曲线的左、右焦点分别为F1,F2,在左支上过F1的弦AB的长为10,若2a=16,则△ABF2的周长是( )
| A. | 32 | B. | 36 | C. | 42 | D. | 52 |
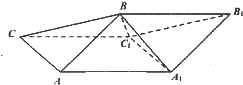 斜三棱柱ABC-A1B1C1中,侧面ABB1A1⊥侧面ACC1A1,A1B=AB=AA1=AC=2,四边形ACC1A1的面积为2$\sqrt{3}$,且∠AA1C1为锐角.
斜三棱柱ABC-A1B1C1中,侧面ABB1A1⊥侧面ACC1A1,A1B=AB=AA1=AC=2,四边形ACC1A1的面积为2$\sqrt{3}$,且∠AA1C1为锐角.