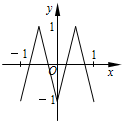题目内容
15.已知f(x)的定义域与值域均为(0,+∞),且f(x)为单调函数,对任意正实数均满足f(f(x)+2)=$\frac{1}{f(x)}$,则f($\frac{1}{2}$)=$-\frac{2}{3}$.分析 利用函数的单调性以及函数的定义域与值域关系,通过换元法变形求解,推出结果.
解答 解:f(x)的定义域与值域均为(0,+∞),且f(x)为单调函数,对任意正实数均满足f(f(x)+2)=$\frac{1}{f(x)}$,
令f(x)=t,
可得f(t+2)=$\frac{1}{t}$,当t=-$\frac{3}{2}$时,f(-$\frac{3}{2}$+2)=$-\frac{2}{3}$,
故答案为:$-\frac{2}{3}$.
点评 本题考查抽象函数的应用,函数值的求法,考查转化思想的应用.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
3.已知正项等比数列{an}满足a7=a6+2a5,若am,an满足$\sqrt{{a}_{m}{a}_{n}}$=8a1,则$\frac{1}{m}$+$\frac{9}{n}$的最小值为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
10.已知0<m<1,设a=logm(m2+1),b=logm(m+1),c=logm(2m),则a,b,c的大小关系是( )
| A. | c>a>b | B. | a>c>b | C. | a>b>c | D. | b>a>c |
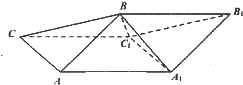 斜三棱柱ABC-A1B1C1中,侧面ABB1A1⊥侧面ACC1A1,A1B=AB=AA1=AC=2,四边形ACC1A1的面积为2$\sqrt{3}$,且∠AA1C1为锐角.
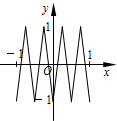
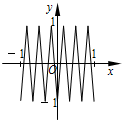
斜三棱柱ABC-A1B1C1中,侧面ABB1A1⊥侧面ACC1A1,A1B=AB=AA1=AC=2,四边形ACC1A1的面积为2$\sqrt{3}$,且∠AA1C1为锐角.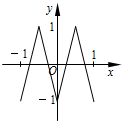 如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )