题目内容
4.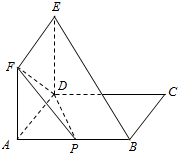 如图所示:矩形ABCD与正方形ADEF所在的平面互相垂直,AB=2AD=4,点P为AB的中点.
如图所示:矩形ABCD与正方形ADEF所在的平面互相垂直,AB=2AD=4,点P为AB的中点.(1)求证:BE∥平面PDF.
(2)求点B到平面PDF的距离.
分析 (1)连接AE,与DF交于O,连接OP,证明OP∥BE,即可证明BE∥平面PDF.
(2)利用等体积法,即可求点B到平面PDF的距离.
解答 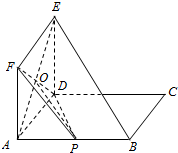 (1)证明:连接AE,与DF交于O,连接OP,则O是AE的中点,
(1)证明:连接AE,与DF交于O,连接OP,则O是AE的中点,
∵点P为AB的中点,
∴OP∥BE,
∵BE?平面PDF,OP?平面PDF,
∴BE∥平面PDF
(2)解:设点B到平面PDF的距离为h,则
△PDF中,PF=DF=PD=2$\sqrt{2}$,S△PDF=2$\sqrt{3}$,
∴由等体积可得$\frac{1}{3}×\frac{1}{2}×2×2×2=\frac{1}{3}×2\sqrt{3}h$,
∴h=$\frac{2\sqrt{3}}{3}$.
点评 本题考查线面平行的判定,考查点B到平面PDF的距离,正确运用线面平行的判定定理是关键.

练习册系列答案
相关题目
16.若函数f(x)在R上可导,且f(x)>f′(x),则当a>b时,下列不等式成立的是( )
| A. | eaf(a)>ebf(b) | B. | ebf(a)>eaf(b) | C. | ebf(b)>eaf(a) | D. | eaf(b)>ebf(a) |
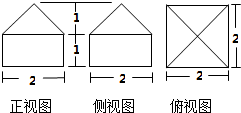 已知一几何体的三视图如图所示.
已知一几何体的三视图如图所示.